

 (AP+AE)d=
(AP+AE)d= (BE+BQ)d=
(BE+BQ)d= (CQ+CF)d=
(CQ+CF)d= (PD+DF)d,
(PD+DF)d,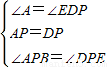


科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2013-2014學年江蘇泰州永安初級中學九年級上學期期中考試數學試卷(解析版) 題型:解答題
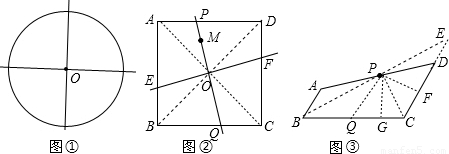
問題探究:
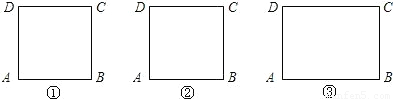
(1)請在圖①中作出兩條直線,使它們將圓面四等分;

(2)如圖②,M是正方形ABCD內一定點,請在圖②中作出兩條直線(要求其中一條直線必須過點M)使它們將正方形ABCD的面積四等分,并說明理由.

問題解決:
(3)如圖③,在四邊形ABCD中,AB∥CD,AB+CD=BC,點P是AD的中點,如果AB=a,CD=b,且b>a,那么在邊BC上是否存在一點Q,使PQ所在直線將四邊形ABCD的面積分成相等的兩部分?如若存在,求出BQ的長;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源:2009-2010學年江蘇省南京市一中分校實驗中學九年級(上)月考數學試卷(12月份)(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2012年廣東省中考數學模擬試卷(九)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com