
【題目】如圖,在四邊形ABCD中,AB=DC,E,F,G,H分別是AD,BC,BD,AC的中點.
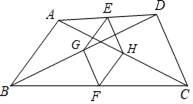
(1)證明:EG=EH;(2)證明:四邊形EHFG是菱形.
【答案】(1)見解析;(2)見解析.
【解析】
(1)利用EG是△ABD的中位線,EH是△ADC的中位線,則有EG=![]() AB,EH=
AB,EH=![]() CD,又AB=CD,可證EG=EH,即可解題.
CD,又AB=CD,可證EG=EH,即可解題.
(2)首先運用三角形中位線定理可得到EG∥AB,HF∥AB,EH∥CD,FE∥DC,從而再根據平行于同一條直線的兩直線平行得到GF∥EH,GE∥FH,可得到GFHE是平行四邊形,再運用三角形中位線定理證明鄰邊相等,從而證明它是菱形.
解:證明:(1)∵四邊形ABCD中,點F、E、G、H分別是BC、AD、BD、AC的中點,
∴EG是△ABD的中位線,EH是△ADC的中位線,
∴EG=![]() AB,EH=
AB,EH=![]() CD,
CD,
∵AB=CD,
∴EG=EH;
(2)∵四邊形ABCD中,點F、E、G、H分別是BC、AD、BD、AC的中點,
∴EG∥AB,HF∥AB,EH∥CD,FE∥DC,
∴GF∥EH,GE∥FH(平行于同一條直線的兩直線平行);
∴四邊形GFHE是平行四邊形,
∵四邊形ABCD中,點E、F、G、H分別是BC、AD、BD、AC的中點,
∴EG是△ABD的中位線,GF是△BCD的中位線,
∴GE=![]() AB,GF=
AB,GF=![]() CD,
CD,
∵AB=CD,
∴GE=GF,
∴四邊形EHFG是菱形.


科目:初中數學 來源: 題型:
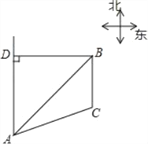
【題目】已知B港口位于A觀測點的東北方向,且其到A觀測點正北方向的距離BD的長為16千米,一艘貨輪從B港口以48千米/時的速度沿如圖所示的BC方向航行,15分后到達C處,現測得C處位于A觀測點北偏東75°方向,求此時貨輪與A觀測點之間的距離AC的長(精確大0.1千米)(參考數據:![]() 1.41,
1.41,![]() 1.73,
1.73,![]() 2.24,
2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在寬20米,長32米的矩形土地上,修筑橫向、縱向道路各一條,且它們互相垂直,若縱向道路的寬是橫向道路的寬的2倍,要使剩余土地的面積為504平方米,求橫向道路的寬為多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是小強洗漱時的側面示意圖,洗漱臺(矩形ABCD)靠墻擺放,高AD=80cm,寬AB=48cm,小強身高166cm,下半身FG=100cm,洗漱時下半身與地面成80°(∠FGK=80°),身體前傾成125°(∠EFG=125°),腳與洗漱臺距離GC=15cm(點D,C,G,K在同一直線上).
(1)此時小強頭部E點與地面DK相距多少?
(2)小強希望他的頭部E恰好在洗漱盆AB的中點O的正上方,他應向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,結果精確到0.1cm)
≈1.41,結果精確到0.1cm)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把所有正偶數從小到大排列,并按如下規律分組:
第一組:2,4;
第二組:6,8,10,12;
第三組:14,16,18,20,22,24
第四組:26,28,30,32,34,36,38,40
……
則現有等式Am=(i,j)表示正偶數m是第i組第j個數(從左到右數),如A10=(2,3),則A2018=( )
A. (31,63) B. (32,17) C. (33,16) D. (34,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【探索發現】
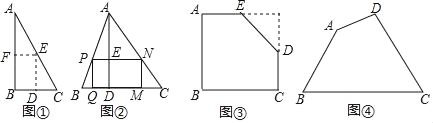
如圖①,是一張直角三角形紙片,∠B=90°,小明想從中剪出一個以∠B為內角且面積最大的矩形,經過多次操作發現,當沿著中位線DE、EF剪下時,所得的矩形的面積最大,隨后,他通過證明驗證了其正確性,并得出:矩形的最大面積與原三角形面積的比值為 .
【拓展應用】
如圖②,在△ABC中,BC=a,BC邊上的高AD=h,矩形PQMN的頂點P、N分別在邊AB、AC上,頂點Q、M在邊BC上,則矩形PQMN面積的最大值為 .(用含a,h的代數式表示)
【靈活應用】
如圖③,有一塊“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明從中剪出了一個面積最大的矩形(∠B為所剪出矩形的內角),求該矩形的面積.
【實際應用】
如圖④,現有一塊四邊形的木板余料ABCD,經測量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐師傅從這塊余料中裁出了頂點M、N在邊BC上且面積最大的矩形PQMN,求該矩形的面積.
,木匠徐師傅從這塊余料中裁出了頂點M、N在邊BC上且面積最大的矩形PQMN,求該矩形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸上點A表示數字6,點B表示數字﹣4
(1)畫數軸,并在數軸上標出點A與點B;
(2)數軸上一動點C從點A出發,沿數軸的負方向以每秒2個單位長度的速度移動,經過4秒到達點E,數軸上另一動點D從點B出發,沿數軸的正方向以每秒1個單位長度的速度移動,經過8秒到達點F,求出點E與點F所表示的數,并在第(1)題的數軸上標出點E,點F;
(3)在第(2)題的條件下,在數軸上找出點H,使點H到點E距離與點H到點F距離之和為8,請在數軸上直接標出點H.(不需寫出求解過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為配合我市創建省級文明城市,某校對八年級各班文明行為勸導志愿者人數進行了統計,各班統計人數有6名、5名、4名、3名、2名、1名共計六種情況,并制作如下兩幅不完整的統計圖.
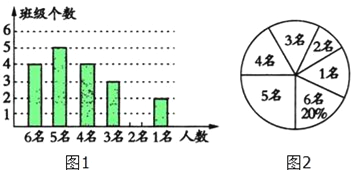
(1)求該年級平均每班有多少文明行為勸導志愿者?并將條形圖補充完整;
(2)該校決定本周開展主題實踐活動,從八年級只有2名文明行為勸導志愿者的班級中任選兩名,請用列表或畫樹狀圖的方法,求出所選文明行為勸導志愿者有兩名來自同一班級的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
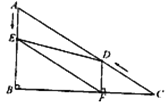
【題目】如圖,在Rt△ABC中,∠B=90°,AB=5,∠C=30°,點D從點C出發沿CA方向以每秒2個單位長的速度向點A勻速運動,同時點E從點A出發沿AB方向以每秒1個單位長的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是t秒(t>0),過點D作DF⊥BC于點F,連接DE、EF.
(1)求證:AE=DF;
(2)四邊形AEFD能夠成為菱形嗎?如果能,求出相應的t值;如果不能,說明理由;
(3)當t為何值時,△DEF為直角三角形?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com