
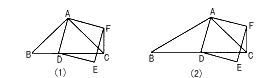
|
解:(1)CF與BD位置關(guān)系是垂直, |
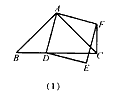 |
| (2)CF⊥BD,(1)中的結(jié)論成立, 理由:如圖(2), 過點A作AC⊥AC交BC于點G ∴AC=AG,仿(1)可證: △GAD≌△CAF, ∴∠ACF=∠AGD=45°, ∠BCF=∠ACB+∠ACF=90° 即CF⊥BO; |
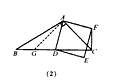 |
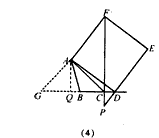
| (3)過點A作AQ上BC交CB的延長線于點Q ①如圖(3)點D在線段BC上運動時, ∵∠BCA=45°, 可求出AQ=CQ=4, ∴DQ =4-x, 易證△AQD∽△DCP, ∴  ∴  ②如圖(4),點D在線段BC延長線上運動時, ∵∠BCA=45°, 可求出AQ=CQ=4, ∴DQ=4+x, 過A作AG⊥AC交CB延長線于點G, 則△AGD≌△ACF, ∴∠AGD=∠ACF, ∵∠AGD+∠ACG=90°, ∴∠ACF+∠ACG=90°, ∴CF⊥ BD, ∴△AQD∽△DCP, 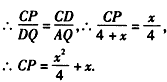 |
  |


 名師點撥卷系列答案
名師點撥卷系列答案科目:初中數(shù)學 來源: 題型:
 如圖所示,在△ABC中,AC與⊙O相切于點A,AC=AB=2,⊙O交BC于D.
如圖所示,在△ABC中,AC與⊙O相切于點A,AC=AB=2,⊙O交BC于D.| 2 |
| 2 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 (2013•松江區(qū)二模)如圖,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江區(qū)二模)如圖,已知在△ABC中,AC=15,AB=25,sin∠CAB=| 4 | 5 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com