
【題目】一組連續奇數按如圖方式排列,請你解決下列問題:
(1)第7行最后一個數字是 , 在第15行第4列的數字是;
(2)請用n的代數式表示第n行的第1個數字和最后一個數字;
(3)現用一個正方形框去圍出相鄰兩行中的4個數字
(例如:第4行和第5行的15,17,23,25),
請問能否在第50行和第51行中 圍出4個數字的和是10016?若能,請求出這4個數字;若不能,請說明理由.
【答案】
(1)55,217
(2)解:第n行的第1個數字為:n-n+1,
最后一個數字為n+n-1;
(3)解:能.因為第50行的第一個數為502-50+1=2451
則第50行第k個數為2451+2k、第k+1個數為2451+2(k+1),
第51行第k個數為2551+2k、第k+1個數為2551+2(k+1),
2451+2k+2451+2(k+1)+2551+2k+2551+2(k+1)=10016,
解得,10008+4k=10016,k=2,
所以這四個數分別為:2453,2455,2553,2555.
【解析】解:(1)∵第六行的最后一個數字為41,
∴第7行最后一個數字為41×2+7=55;
∵第15行第一個數字為1+(1+2+3+……+14)×2=211,
∴第15行第4個數字為211+2×3=217.
(1)根據第六行的最后一個數字,將其+2×7可得第一個空;第15行第一個數字為1+(1+2+3+……+14)×2,將其+2×3可得第二個空;
(2)由所給的數列可得第n行第1個數字,再由第n行最后一個數字為第(n+1)行第一個數字-2可得答案;
(3)根據(2)中得出的結論可求得第50、51行第一個數字,進而可得第50、51行第k、k+1列的四個數字,然后得到關于k的方程,從而解出k的值,進而得到答案.


科目:初中數學 來源: 題型:
【題目】如圖1,在□ABCD中,AE⊥BC于E,E恰為BC的中點,tanB=2。



(1)求證:AD=AE;
(2)如圖2,點P在BE上,作EF⊥DP于點F,連結AF,求證:DF-EF=![]() AF;
AF;
(3)請你在圖3中畫圖探究:當P為射線EC上任意一點(P不與點E重合)時,作EF⊥DP于點F,連結AF,線段DF、EF與AF之間有怎樣的數量關系?直接寫出你的結論為____________。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1所示,已知△ABC中,∠BAC=90°,AB=AC,AE是過點A的一條直線,且B點和C點在AE的異側,BD⊥AE于D點,CE⊥AE與E點.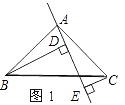
(1)求證:BD=DE+CE
(2)若直線AE繞點A旋轉到圖2所示的位置時(BD<CE)其余條件不變,問BD 與DE,CE的關系如何?請予以證明.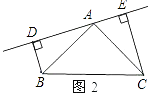
(3)若直線AE繞點A旋轉到圖3所示的位置時(BD>CE)其余條件不變,問BD 與DE,CE的關系如何?直接寫出結果,不需證明.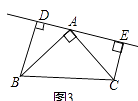
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按下面的程序計算:
當輸入 ![]() 時,輸出結果是299;當輸入
時,輸出結果是299;當輸入 ![]() 時,輸出結果是466;如果輸入
時,輸出結果是466;如果輸入 ![]() 的值是正整數,輸出結果是257,那么滿足條件的
的值是正整數,輸出結果是257,那么滿足條件的 ![]() 的值最多有( )
的值最多有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強公民的節水意識,合理利用水資源,某市采用價格調控的手段達到節水的目的,該市自來水收費的收費標準如下表: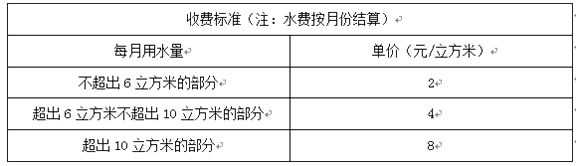
例如:某戶居民1月份用水8立方米,應收水費為2×6+4×(8-6)=20(元).
請根據上表的內容解答下列問題:
(1)若某戶居民2月份用水5立方米,則應收水費元;
(2)若某戶居民3月份交水費36元,則用水量為立方米;
(3)若某戶居民4月份用水a立方米(其中6<a<10),請用含a的代數式表示應收水費元.
(4)若某戶居民 5、6 兩個月共用水18立方米(6月份用水量超過了10立方米),設5月份用水x立方米,請用含x的代數式表示該居民5、6兩個月共交水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七年級進行法律知識競賽,共有30道題,答對一道題得4分,不答或答錯一道題扣2分.
(1)小紅同學參加了競賽,成績是90分,請問小紅在競賽中答對了多少道題?
(2)小明也參加了競賽,考完后他說:“這次競賽我一定能拿到100分.”請問小明有沒有可能拿到100分?試用方程的知識來說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com