
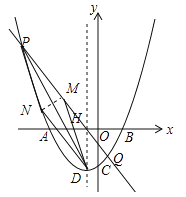
【題目】如圖,在平面直角坐標系xOy中,拋物線![]() 與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C(0,
與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C(0,![]() ),頂點為D,對稱軸與x軸交于點H,過點H的直線l交拋物線于P,Q兩點,點Q在y軸的右側.
),頂點為D,對稱軸與x軸交于點H,過點H的直線l交拋物線于P,Q兩點,點Q在y軸的右側.
(1)求a的值及點A,B的坐標;
(2)當直線l將四邊形ABCD分為面積比為3:7的兩部分時,求直線l的函數表達式;
(3)當點P位于第二象限時,設PQ的中點為M,點N在拋物線上,則以DP為對角線的四邊形DMPN能否為菱形?若能,求出點N的坐標;若不能,請說明理由.

【答案】(1)![]() ,A(-4,0),B(2,0);(2)y=2x+2或
,A(-4,0),B(2,0);(2)y=2x+2或![]() ;(3)存在,N(-
;(3)存在,N(-![]() , 1).
, 1).
【解析】
試題分析:(1)把點C代入拋物線解析式即可求出a,令y=0,列方程即可求出點A、B坐標.
(2)先求出四邊形ABCD面積,分兩種情形:①當直線l邊AD相交與點M1時,根據S△AHM1=![]() ×10=3,求出點M1坐標即可解決問題.②當直線l邊BC相交與點M2時,同理可得點M2坐標.
×10=3,求出點M1坐標即可解決問題.②當直線l邊BC相交與點M2時,同理可得點M2坐標.
(3)設P(![]() ,
,![]() )、Q(
)、Q(![]() ,
,![]() )且過點H(﹣1,0)的直線PQ的解析式為y=kx+b,得到b=k,利用方程組求出點M坐標,求出直線DN解析式,再利用方程組求出點N坐標,列出方程求出k,即可解決問題.
)且過點H(﹣1,0)的直線PQ的解析式為y=kx+b,得到b=k,利用方程組求出點M坐標,求出直線DN解析式,再利用方程組求出點N坐標,列出方程求出k,即可解決問題.
試題解析:(1)∵拋物線與y軸交于點C(0,![]() ),∴a﹣3=
),∴a﹣3=![]() ,解得:
,解得:![]() ,∴
,∴![]()
當y=0時,有![]() ,∴
,∴ ![]() ,
,![]() ,∴A(﹣4,0),B(2,0).
,∴A(﹣4,0),B(2,0).
(2)∵A(﹣4,0),B(2,0),C(0,![]() ),D(﹣1,﹣3)
),D(﹣1,﹣3)
∴S四邊形ABCD=S△ADH+S梯形OCDH+S△BOC=![]() =10.
=10.
從面積分析知,直線l只能與邊AD或BC相交,所以有兩種情況:
①當直線l邊AD相交與點M1時,則S△AHM1=![]() ×10=3,∴
×10=3,∴![]() ×3×(-yM1)=3,∴yM1=-2,點M1(﹣2,﹣2),過點H(﹣1,0)和M1(﹣2,﹣2)的直線l的解析式為y=2x+2.
×3×(-yM1)=3,∴yM1=-2,點M1(﹣2,﹣2),過點H(﹣1,0)和M1(﹣2,﹣2)的直線l的解析式為y=2x+2.
②當直線l邊BC相交與點M2時,同理可得點M2(![]() ,﹣2),過點H(﹣1,0)和M2(
,﹣2),過點H(﹣1,0)和M2(![]() ,﹣2)的直線l的解析式為
,﹣2)的直線l的解析式為![]() .
.
綜上所述:直線l的函數表達式為y=2x+2或![]() .
.
(3)設P(![]() ,
,![]() )、Q(
)、Q(![]() ,
,![]() )且過點H(﹣1,0)的直線PQ的解析式為y=kx+b,∴﹣k+b=0,∴b=k,∴y=kx+k.
)且過點H(﹣1,0)的直線PQ的解析式為y=kx+b,∴﹣k+b=0,∴b=k,∴y=kx+k.
由 ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,∵點M是線段PQ的中點,∴由中點坐標公式的點M(
,∵點M是線段PQ的中點,∴由中點坐標公式的點M(![]() ,
,![]() ).
).
假設存在這樣的N點如圖,直線DN∥PQ,設直線DN的解析式為y=kx+k﹣3,由 ,解得:
,解得:![]() ,
, ![]() , ∴N(
, ∴N(![]() ,
,![]() ).
).
∵四邊形DMPN是菱形,∴DN=DM,∴![]() ,整理得:
,整理得:![]() ,
,![]() ,∵
,∵ ![]() >0,∴
>0,∴![]() ,解得
,解得![]() ,∵k<0,∴
,∵k<0,∴![]() ,∴P(-
,∴P(-![]() ,6),M(-
,6),M(-![]() ,2),N(-
,2),N(-![]() , 1),∴PM=DN=
, 1),∴PM=DN=![]() ,∵PM∥DN,∴四邊形DMPN是平行四邊形,∵DM=DN,∴四邊形DMPN為菱形,∴以DP為對角線的四邊形DMPN能成為菱形,此時點N的坐標為(﹣
,∵PM∥DN,∴四邊形DMPN是平行四邊形,∵DM=DN,∴四邊形DMPN為菱形,∴以DP為對角線的四邊形DMPN能成為菱形,此時點N的坐標為(﹣![]() ,1).
,1).


科目:初中數學 來源: 題型:
【題目】某小組7名同學積極捐出自己的零花錢支援地震災區,他們捐款的數額分別是(單位:元):50,20,50,30,50,25,135.這組數據的眾數和中位數分別是( ).
A.50,20B.50,30C.50,50D.135,50
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年中秋小長假長沙縣的旅游收入約為1900萬,將1900萬用科學記數法表示應為( )
A. 19×104 B. 1.9×104 C. 1.9×107 D. 0.19×108
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠A=100°,BI、CI分別平分∠ABC,∠ACB,則∠BIC=________,若BM、CM分別平分∠ABC,∠ACB的外角平分線,則∠M=__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在△ABC中,BE、CF分別是AC、AB兩邊上的高,在BE上截取BD=AC,在CF的延長線上截取CG=AB,連結AD、AG。
(1)求證:AD=AG
(2)AD與AG的位置關系如何,請說明理由。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第二屆“紅色日記”征文大賽于2020年1月12日正式啟動,征文內容分為兩部分:“不忘初心”和“紅色傳承”.其中五位評委給參賽者小亮的征文評分分別為:88、92、90、93、88,則這組數據的眾數是 ( )
A.88B.90C.92D.93
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com