
 )和(0,-
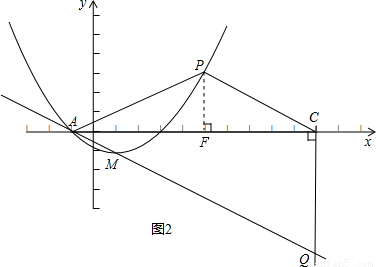
)和(0,- ).點P(x,y)在拋物線的頂點M的右側的半支上(包括頂點M),在x軸上有一點C使△OPC是等腰三角形,OP=PC.
).點P(x,y)在拋物線的頂點M的右側的半支上(包括頂點M),在x軸上有一點C使△OPC是等腰三角形,OP=PC.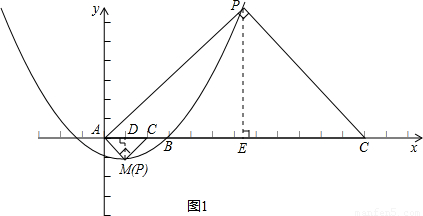 解法一:
解法一: ),(0,-
),(0,- ),
),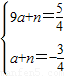 ,
,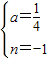 ;
;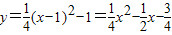 ;
;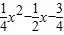 =0,
=0,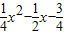 ,
,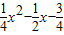
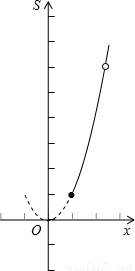
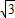 (舍負),
(舍負),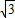 ,
,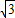 ,3+2
,3+2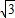 ).
).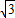 ,3+2
,3+2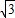 );
);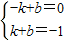 ,
,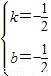 ;
; x-
x- ,
,
 ),
), AC•CQ
AC•CQ |2x-(-1)|•|0-(-x-
|2x-(-1)|•|0-(-x- )|
)| (2x+1)(x+
(2x+1)(x+ )
) )2
)2 ;
;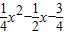 上,
上,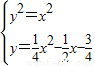 ;
;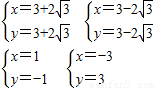
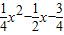 的頂點M的右側的半支上(包括頂點M),∠OPC是直角,
的頂點M的右側的半支上(包括頂點M),∠OPC是直角,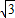 ,3+2
,3+2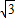 ),或(1,-1).
),或(1,-1).

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:2002年北京市朝陽區中考數學試卷(解析版) 題型:解答題
 )和(0,-
)和(0,- ).點P(x,y)在拋物線的頂點M的右側的半支上(包括頂點M),在x軸上有一點C使△OPC是等腰三角形,OP=PC.
).點P(x,y)在拋物線的頂點M的右側的半支上(包括頂點M),在x軸上有一點C使△OPC是等腰三角形,OP=PC.查看答案和解析>>
科目:初中數學 來源:2002年全國中考數學試題匯編《銳角三角函數》(04)(解析版) 題型:解答題
 時,sinB=
時,sinB= ;
; 時,sinB=
時,sinB= (提示:
(提示: =
= );
); 時,sinB=
時,sinB= .
. 時,sinB的值等于______
時,sinB的值等于______查看答案和解析>>
科目:初中數學 來源:2002年全國中考數學試題匯編《銳角三角函數》(02)(解析版) 題型:選擇題



查看答案和解析>>
科目:初中數學 來源:2002年全國中考數學試題匯編《圖形的相似》(06)(解析版) 題型:解答題
 ,EH-HF=2.設∠ACB=a,tana=
,EH-HF=2.設∠ACB=a,tana= ,EH和HF是方程x2-(k+2)x+4k=0的兩個實數根.
,EH和HF是方程x2-(k+2)x+4k=0的兩個實數根.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com