
【題目】如圖,將半徑為2,圓心角為![]() 的扇形OAB繞點A逆時針旋轉
的扇形OAB繞點A逆時針旋轉![]() ,點O,B的對應點分別為
,點O,B的對應點分別為![]() ,
, ![]() ,連接
,連接![]() ,則圖中陰影部分的面積是
,則圖中陰影部分的面積是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:連接OO′,BO′,根據旋轉的性質得到∠OAO′=60°,推出△OAO′是等邊三角形,得到∠AOO′=60°,推出△OO′B是等邊三角形,得到∠AO′B=120°,得到∠O′B′B=∠O′BB′=30°,根據圖形的面積公式即可得到結論.
詳解:連接OO′,BO′,
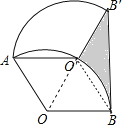
∵將半徑為2,圓心角為120°的扇形OAB繞點A逆時針旋轉60°,
∴∠OAO′=60°,
∴△OAO′是等邊三角形,
∴∠AOO′=60°,OO′=OA,
∴點O′中⊙O上,
∵∠AOB=120°,
∴∠O′OB=60°,
∴△OO′B是等邊三角形,
∴∠AO′B=120°,
∵∠AO′B′=120°,
∴∠B′O′B=120°,
∴∠O′B′B=∠O′BB′=30°,
∴圖中陰影部分的面積=S△B′O′B-(S扇形O′OB-S△OO′B)=![]() ×1×2
×1×2![]() -(
-(![]() -
-![]() ×2×
×2×![]() )=2
)=2![]() -
- ![]() .
.
故選C.


科目:初中數學 來源: 題型:
【題目】已知OC是∠AOB內部的一條射線,M,N分別為OA,OC上的點,線段OM,ON同時分別以30°/s,10°/s的速度繞點O逆時針旋轉,設旋轉時間為t秒.
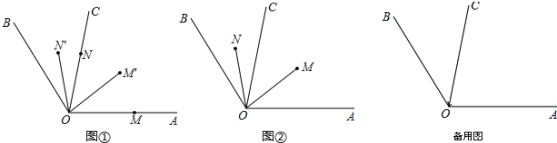
(1)如圖①,若∠AOB=120°,當OM、ON逆時針旋轉到OM′、ON′處,
①若OM,ON旋轉時間t為2時,則∠BON′+∠COM′= °;
②若OM′平分∠AOC,ON′平分∠BOC,求∠M′ON′的值;
(2)如圖②,若∠AOB=4∠BOC,OM,ON分別在∠AOC,∠BOC內部旋轉時,請猜想∠COM與∠BON的數量關系,并說明理由.
(3)若∠AOC=80°,OM,ON在旋轉的過程中,當∠MON=20°,t= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,以AC為直徑作⊙O,交AB于D,過點O作OE∥AB,交BC于E.
(1)求證:ED為⊙O的切線;
(2)如果⊙O的半徑為![]() ,ED=2,延長EO交⊙O于F,連接DF、AF,求△ADF的面積.
,ED=2,延長EO交⊙O于F,連接DF、AF,求△ADF的面積.

【答案】(1)證明見解析;(2)![]()
【解析】試題分析:(1)首先連接OD,由OE∥AB,根據平行線與等腰三角形的性質,易證得![]() ≌
≌![]() 即可得
即可得![]() ,則可證得
,則可證得![]() 為
為![]() 的切線;
的切線;
(2)連接CD,根據直徑所對的圓周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的長,又由OE∥AB,證得
的長,又由OE∥AB,證得![]() 根據相似三角形的對應邊成比例,即可求得
根據相似三角形的對應邊成比例,即可求得![]() 的長,然后利用三角函數的知識,求得
的長,然后利用三角函數的知識,求得![]() 與
與![]() 的長,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的長,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
試題解析:(1)證明:連接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切線;
的切線;
(2)連接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直徑,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面積為![]()

【題型】解答題
【結束】
25
【題目】【題目】已知,拋物線y=ax2+ax+b(a≠0)與直線y=2x+m有一個公共點M(1,0),且a<b.
(1)求b與a的關系式和拋物線的頂點D坐標(用a的代數式表示);
(2)直線與拋物線的另外一個交點記為N,求△DMN的面積與a的關系式;
(3)a=﹣1時,直線y=﹣2x與拋物線在第二象限交于點G,點G、H關于原點對稱,現將線段GH沿y軸向上平移t個單位(t>0),若線段GH與拋物線有兩個不同的公共點,試求t的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點![]() 表示的數為
表示的數為![]() ,點
,點![]() 表示的數為
表示的數為![]() ,以
,以![]() 為邊在數軸的上方作正方形ABCD.動點
為邊在數軸的上方作正方形ABCD.動點![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位長度的速度沿數軸正方向勻速運動,同時動點
個單位長度的速度沿數軸正方向勻速運動,同時動點![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位長度的速度向點
個單位長度的速度向點![]() 勻速運動,到達
勻速運動,到達![]() 點后再以同樣的速度沿數軸正方向勻速運動,設運動時間為
點后再以同樣的速度沿數軸正方向勻速運動,設運動時間為![]() 秒
秒![]() .
.
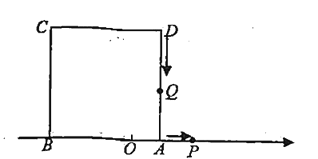
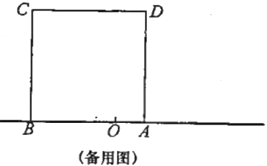
(1)若點![]() 在線段
在線段![]() .上運動,當t為何值時,
.上運動,當t為何值時,![]() ?
?
(2)若點![]() 在線段
在線段![]() 上運動,連接
上運動,連接![]() ,當t為何值時,三角形
,當t為何值時,三角形![]() 的面積等于正方形
的面積等于正方形![]() 面積的
面積的![]() ?
?
(3)在點![]() 和點
和點![]() 運動的過程中,當
運動的過程中,當![]() 為何值時,點
為何值時,點![]() 與點
與點![]() 恰好重合?
恰好重合?
(4)當點![]() 在數軸上運動時,是否存在某-時刻t,使得線段
在數軸上運動時,是否存在某-時刻t,使得線段![]() 的長為
的長為![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
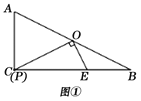
【題目】已知:在Rt△ABC中,∠ACB=90°,AC=4,BC=8,O是AB邊的中點,P是AC邊上的動點,OE⊥OP交BC邊于點E,連接PE.
(1)如圖①,當P與C重合時,線段PE的長為___________;
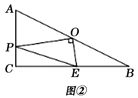
(2)如圖②,當P在AC邊上運動時,
①探究:線段PA,PE,EB之間的數量關系,并證明你的結論;
②若設PA=![]() ,PE2=y,求y與x之間的函數關系式及線段PE的最小值.
,PE2=y,求y與x之間的函數關系式及線段PE的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在綜合與實踐課上,老師組織同學們以“矩形紙片的折疊”為主題開展數學活動.
(1)奮進小組用圖1中的矩形紙片ABCD,按照如圖2所示的方式,將矩形紙片沿對角線AC折疊,使點B落在點![]() 處,則
處,則![]() 與
與![]() 重合部分的三角形的類型是________.
重合部分的三角形的類型是________.
(2)勤學小組將圖2中的紙片展平,再次折疊,如圖3,使點A與點C重合,折痕為EF,然后展平,則以點A、F、C、E為頂點的四邊形是什么特殊四邊形?請說明理由.
(3)創新小組用圖4中的矩形紙片ABCD進行操作,其中![]() ,
,![]() ,先沿對角線BD對折,點C落在點
,先沿對角線BD對折,點C落在點![]() 的位置,
的位置,![]() 交AD于點G,再按照如圖5所示的方式折疊一次,使點D與點A重合,得折痕EN,EN交AD于點M.則EM的長為________cm.
交AD于點G,再按照如圖5所示的方式折疊一次,使點D與點A重合,得折痕EN,EN交AD于點M.則EM的長為________cm.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電動車廠一周計劃生產2100輛電動車,平均每天計劃生產300輛,由于各種原因,實際每天的生產量與計劃量相比有出入.下表是某周的生產情況(超產為正,減產為負).
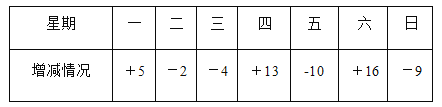
(1)根據記錄可知本周前三天共生產電動車多少輛?
(2)本周產量最多的一天比產量最少的一天多生產電動車多少輛?
(3)該廠實行每周計件工資制,每生產一輛電動車可得a元,若超額完成,則超額部分每輛再獎b元(b<a),少生產一輛扣b元,求該廠工人這一周的工資總額.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某劇院的觀眾席的座位為扇形,且按下列分式設置:
排數(x) | 1 | 2 | 3 | 4 | … |
座位數(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的規律,當x每增加1時,y如何變化?
(2)寫出座位數y與排數x之間的關系式;
(3)按照上表所示的規律,某一排可能有90個座位嗎?說說你的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com