
【題目】如圖,在每個邊長為1的小正方形的網格中,△ABC的頂點A,B,C在格點上,P是BC邊上任意一點,以A為中心,取旋轉角等于∠BAC,把點P逆時針旋轉,點P的對應點為點P',當CP'最短時,畫出點P',并說明CP'最短的理由是______.
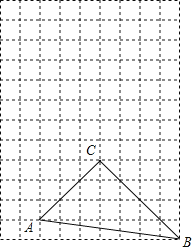
【答案】垂線段最短.
【解析】
連CF,根據已知條件得到A、C、F共線,求得AF=5![]() =AB,根據相似三角形的想知道的∠GFC=∠B,求得∠TCA=∠TAC,得到CP′⊥GF,于是得到結論.
=AB,根據相似三角形的想知道的∠GFC=∠B,求得∠TCA=∠TAC,得到CP′⊥GF,于是得到結論.
解:作圖過程如下:
取格點D,E,連接DE交AB于點T;取格點M,N,連接MN交BC延長線于點G:取格點F,連接FG交TC延長線于點P′,則點P′即為所求
證明:連CF,
∵AC,CF為正方形網格對角線
∴A、C、F共線
∴AF=5![]() =AB,
=AB,
由圖形可知:GC=![]() ,CF=2
,CF=2![]() ,
,
∵AC=![]() =3
=3![]() ,BC=4
,BC=4![]() ,
,
∴△ACB∽△GCF,
∴∠GFC=∠B,
∵AF=5![]() =AB,
=AB,
∴當BC邊繞點A逆時針旋轉∠CAB時,點B與點F重合,點C在射線FG上.
由作圖可知T為AB中點,
∴∠TCA=∠TAC,
∴∠F+∠P′CF=∠B+∠TCA=∠B+∠TAC=90°,
∴CP′⊥GF,
此時,CP′最短,
故答案為垂線段最短.


科目:初中數學 來源: 題型:
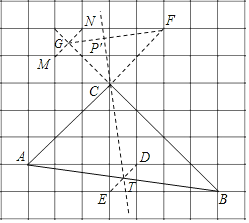
【題目】如圖,在每個小正方形的邊長為的網格中,點![]() 均在格點上,
均在格點上,![]() 為小正方形邊中點.
為小正方形邊中點.
(1)![]() 的長等于 ______;
的長等于 ______;
(2)請在如圖所示的網格中,用無刻度的直尺,畫出一個點![]() ,使其滿足
,使其滿足![]() 說明點
說明點![]() 的位置是如何找到的(不要求證明)______.
的位置是如何找到的(不要求證明)______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,二次函數![]() 的圖像經過點
的圖像經過點![]() ,點
,點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,
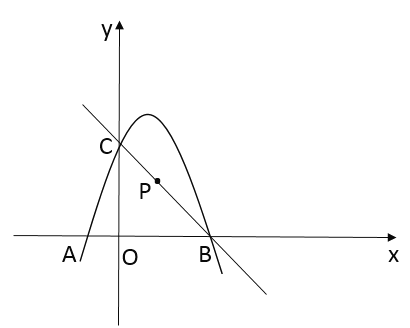
(1)求![]() 、
、![]() 的值:
的值:
(2)若點![]() 為直線
為直線![]() 上一點,點
上一點,點![]() 到直線
到直線![]() 、
、![]() 兩點的距離相等,將該拋物線向左(或向右)平移,得到一條新拋物線,并且新拋物線經過點
兩點的距離相等,將該拋物線向左(或向右)平移,得到一條新拋物線,并且新拋物線經過點![]() ,求新拋物線的頂點坐標.
,求新拋物線的頂點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】受疫情的影響,很多農產品滯銷,各大電商發起了“愛心助農”活動,幫助農戶進行農產品銷售.已知某種橘子的成本為4元/千克,經過市場調查發現,一天內橘子的銷售量y(千克)與銷售單價x(元/千克)(4≤x≤10)的函數關系如下圖所示:

(1)當4≤x≤8時,求y與x的函數解析式;
(2)當4≤x≤8時,要使一天內獲得的利潤為1200元,單價應定為多少?
(3)求橘子的單價定為多少時,一天內獲得的利潤最大,最大利潤為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中華文明,源遠流長;中華漢字,寓意深廣.為了傳承中華民族優秀傳統文化,我市某中學舉行“漢字聽寫”比賽,賽后整理參賽學生的成績,將學生的成績分為A,B,C,D四個等級,并將結果繪制成如圖所示的條形統計圖和扇形統計圖,但均不完整.

請你根據統計圖解答下列問題:
(1)參加比賽的學生共有____名;
(2)在扇形統計圖中,m的值為____,表示“D等級”的扇形的圓心角為____度;
(3)組委會決定從本次比賽獲得A等級的學生中,選出2名去參加全市中學生“漢字聽寫”大賽.已知A等級學生中男生有1名,請用列表法或畫樹狀圖法求出所選2名學生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C = 90°, P是CB邊上一動點,連接AP,作PQ⊥AP交AB于Q . 已知AC = 3cm,BC = 6cm,設PC的長度為xcm,BQ的長度為ycm .

小青同學根據學習函數的經驗對函數y隨自變量x的變化而變化的規律進行了探究.
下面是小青同學的探究過程,請補充完整:
(1) 按照下表中自變量x的值進行取點、畫圖、測量,分別得到了y的幾組對應值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(說明:補全表格時,相關數據保留一位小數)
m的值約為多少cm;
(2)在平面直角坐標系中,描出以補全后的表格中各組數值所對應的點(x ,y),畫出該函數的圖象;

(3)結合畫出的函數圖象,解決問題:
①當y > 2時,寫出對應的x的取值范圍;
②若點P不與B,C兩點重合,是否存在點P,使得BQ=BP?(直接寫結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
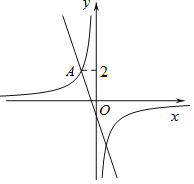
【題目】如圖,在平面直角坐標系xOy中,直線![]() 與雙曲線
與雙曲線![]() 相交于點
相交于點![]() .
.
![]() 求雙曲線
求雙曲線![]() 的表達式;
的表達式;
![]() 過動點
過動點![]() 且垂直于x軸的直線與直線
且垂直于x軸的直線與直線![]() 及雙曲線
及雙曲線![]() 的交點分別為B和C,當點B位于點C下方時,求出n的取值范圍.
的交點分別為B和C,當點B位于點C下方時,求出n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個函數當自變量在不同范圍內取值時,函數表達式不同,我們稱這樣的函數為分段函數.下面我們參照學習函數的過程與方法,探究分段函數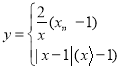 的圖象與性質.列表:
的圖象與性質.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描點:在平面直角坐標系中,以自變量x的取值為橫坐標,以相應的函數值y為縱坐標,描出相應的點,如圖所示.
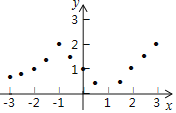
(1)如圖,在平面直角坐標系中,觀察描出的這些點的分布,作出函數圖象;
(2)研究函數并結合圖象與表格,回答下列問題:
①點![]() ,
,![]() ,
,![]() ,
,![]() 在函數圖象上,
在函數圖象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②當函數值![]() 時,求自變量x的值;
時,求自變量x的值;
③在直線![]() 的右側的函數圖象上有兩個不同的點
的右側的函數圖象上有兩個不同的點![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直線![]() 與函數圖象有三個不同的交點,求a的取值范圍.
與函數圖象有三個不同的交點,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
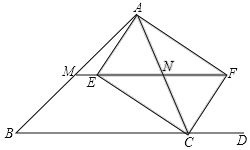
【題目】如圖:在△ABC中,CE、CF分別平分∠ACB與它的鄰補角∠ACD,AE⊥CE于E,AF⊥CF于F,直線EF分別交AB、AC于M、N.
(1)求證:四邊形AECF為矩形;
(2)試猜想MN與BC的關系,并證明你的猜想;
(3)如果四邊形AECF是菱形,試判斷△ABC的形狀,直接寫出結果,不用說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com