
【題目】如圖,在![]() 中,
中,![]() 于
于![]() ,且
,且![]() .
.
(![]() )求證:
)求證:![]() .
.
(![]() )若
)若![]() ,
,![]() 于
于![]() ,
,![]() 為
為![]() 中點,
中點,![]() 與
與![]() ,
,![]() 分別交于點
分別交于點![]() ,
,![]() .
.
①判斷線段![]() 與
與![]() 相等嗎?請說明理由.
相等嗎?請說明理由.
②求證:![]() .
.

【答案】見解析
【解析】試題分析:(1)根據SAS證明△ABE≌△CBE,即可得結論;(2)①BH=AC,根據已知條件求出∠BCD=∠ABC,∠ABE=∠DCA,推出DB=CD,根據ASA證出△DBH≌△DCA,即可得結論;②連接CG,AG,根據AB=BC,BE⊥AC,可得BE垂直平分AC,根據線段垂直平分線的性質可得AG=CG,再由F點是BC的中點,DB=DC,可得DF垂直平分BC,所以BG=CG,即可得AG=BG,在Rt△AEG中,由勾股定理即可推出答案.
試題解析:
(![]() )證明:在
)證明:在![]() 與
與![]() 中,
中,
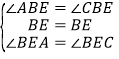 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
(![]() )①
)①![]() ,
,
理由:∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 與
與![]() 中,
中,
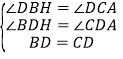 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
②證明:如圖,連接![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
∵![]() 點是
點是![]() 的中點,
的中點,![]() ,
,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.



 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖:在平行四邊形ABCD中,用直尺和圓規作∠BAD的平分線交BC于點E(尺規作圖的痕跡保留在圖中了),連接EF.
(1)求證:四邊形ABEF為菱形;
(2)AE,BF相交于點O,若BF=6,AB=5,求AE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,DE分別是AB,AC的中點,BE=2DE,延長DE到點F,使得EF=BE,連CF
(1)求證:四邊形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,直線y=﹣x+2與反比例函數y=![]() 的圖象有唯一公共點,若直線y=﹣x+b與反比例函數y=
的圖象有唯一公共點,若直線y=﹣x+b與反比例函數y=![]() 的圖象有2個公共點,則b的取值范圍是( )
的圖象有2個公共點,則b的取值范圍是( )

A. b>2 B. ﹣2<b<2 C. b>2或b<﹣2 D. b<﹣2
查看答案和解析>>
科目:初中數學 來源: 題型:
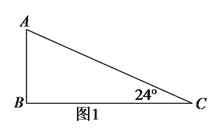
【題目】(![]() )如圖
)如圖![]() 中,
中,![]() ,請用直尺和圓規作一條直線,把
,請用直尺和圓規作一條直線,把![]() 分割成兩個等腰三角形(不寫作法,但須保留作圖痕跡).
分割成兩個等腰三角形(不寫作法,但須保留作圖痕跡).
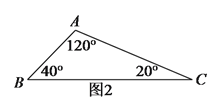
(![]() )如圖
)如圖![]() 中,
中,![]() 的三個內角分別為
的三個內角分別為![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,在
,在![]() 上找一個點
上找一個點![]() ,使
,使![]() 為等腰三角形,求出
為等腰三角形,求出![]() 的長(可用含
的長(可用含![]() 的代數式表示).
的代數式表示).


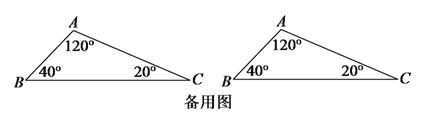
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若動點
,若動點![]() 從點
從點![]() 開始,按
開始,按![]() 的路徑
的路徑![]() 運動一周,且速度為每秒
運動一周,且速度為每秒![]() ,設運動的時間為
,設運動的時間為![]() 秒.
秒.
(![]() )求
)求![]() 為何值時,
為何值時,![]() 把
把![]() 的周長分成相等的兩部分
的周長分成相等的兩部分
(![]() )求
)求![]() 為何值時,
為何值時,![]() 把
把![]() 的面積分成相等的兩部分;并求此時
的面積分成相等的兩部分;并求此時![]() 的長.
的長.
(![]() )求
)求![]() 為何值時,
為何值時,![]() 為等腰三角形?(請直接寫出答案)
為等腰三角形?(請直接寫出答案)


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分13分)在平面直角坐標系中,O為原點,直線y =-2x-1與y軸交于點A,與直線y =-x交于點B,點B關于原點的對稱點為點C.

(1)求過A,B,C三點的拋物線的解析式;
(2)P為拋物線上一點,它關于原點的對稱點為Q.
①當四邊形PBQC為菱形時,求點P的坐標;
②若點P的橫坐標為t(-1<t<1),當t為何值時,四邊形PBQC面積最大,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若x、y是有理數,設N=3x2+2y2﹣18x+8y+35,則N( )
A. 一定是負數 B. 一定不是負數 C. 一定是正數 D. N的取值與x、y的取值有關
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com