
如圖,Rt△ABC中,∠C= Rt∠,AC=BC=2,E,F分別為AC,AB的中點,連結EF。
現將一把直角尺放在給出的圖形上,使直角頂點P在線段EF(包括端點)上滑動,直角的
一邊始終經過點C,另一邊與BF相交于G,連結AP。
(1)求證:PC=PA=PG;
(2)設EP=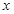 ,四邊形BCPG的面積為
,四邊形BCPG的面積為 ,求
,求 與
與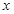 之間的函數解析式,現有三個數
之間的函數解析式,現有三個數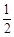 ,
, ,
,
 試通過計算說明哪幾個數符合
試通過計算說明哪幾個數符合 值的要求,并求出符合
值的要求,并求出符合 值時的
值時的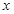 的值。
的值。
(3)當直角頂點P滑動到點F時,再將直角尺繞點F順時針旋轉,兩直角邊分別交AC,BC于點M,N,連結MN。當旋轉到使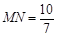 時,求△APM的周長。
時,求△APM的周長。


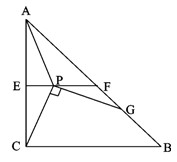
(1)∵E,F分別是AC,AB的中點,∴EF= ,EF∥BC,
,EF∥BC,
∴EF垂直平分AC,∴AP=PC,
∠ECP=∠EAP;∵∠CPG=90°,∴∠ECP+∠EPC=∠GPF+∠EPC
∴∠ECP=∠GPF。∵∠GPF+∠PGF=∠AFE=45°,
∠EAP+∠PAF=45°,∴∠PGF=∠PAF。
∴PA=PG,∴PA=PC=PG。
(2)過G作PF的垂線,垂足為H,
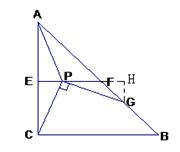
∵ ∠ECP+∠EPC=90°,∠HPG+∠EPC=90°∴∠ECP=∠HPH, PC=PG。
則R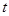 △PCE≌R
△PCE≌R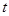 △GPH(AAS),∴GH=PE=
△GPH(AAS),∴GH=PE=
∴ ,
,
∴  ,或
,或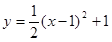 。
。
∵0≤ <1,∴1<
<1,∴1<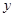 ≤
≤ 。∴
。∴ ,
, 不符合,所以只有
不符合,所以只有 ,
,
∴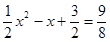 ,
,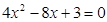 ,解得,
,解得, ,
, >1(舍去),
>1(舍去),
答當 時,
時,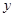 的值為
的值為 。
。
或①當 時,
時,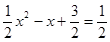 ,△<0,方程無實數解;
,△<0,方程無實數解;
②當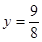 時,
時,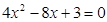 ,解得,
,解得, ,
, >1(舍去),
>1(舍去),
所以當 時,
時,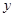 的值為
的值為 。
。
③當 時,
時, ,解得
,解得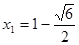 <0(舍去),
<0(舍去), >1(舍去),所以不符合。
>1(舍去),所以不符合。
(2)連結CP,則CP⊥AB,
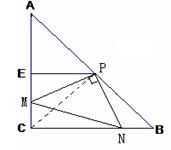
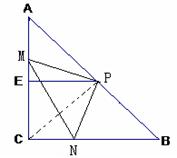
∵AP=CP,∠A=∠PCN=45°,
∠APM+∠MPC=∠CPN+∠MPN=90°,∴∠APM=∠CPN,△APM≌△CPN(ASA), AM=CN,
則CN=BN, ,則
,則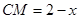 ,
,
 ,解得,
,解得, ,
,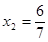 ,即
,即 或
或 ;
;
∴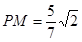 ,
, ,
∴周長為
,
∴周長為 ,或
,或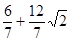
【解析】(1)先利用EF垂直平分AC得出AP=PC,再利用等量代換得出∠PGF=∠PAF得出PA=PG,從而得出PA=PC=PG;
(2)過G點作PF的垂線,垂足為H,證出R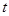 △PCE≌R
△PCE≌R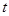 △GPH,得出GH=PE=
△GPH,得出GH=PE= ,然后利用四邊形BCPG面積=梯形BCEF面積-△CEP面積-△PFG面積得出解析式,然后根據0≤
,然后利用四邊形BCPG面積=梯形BCEF面積-△CEP面積-△PFG面積得出解析式,然后根據0≤ <1,得出y的取值范圍,再把已知的三個數代入求解;
<1,得出y的取值范圍,再把已知的三個數代入求解;
(3)連接CP,證出△APM≌△CPN,得出AM=CN,然后利用△MNC為直角三角形,算出CM的長,即AM的長,再計算出AP和PM的長,從而得出△APM的周長。


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,Rt△ABC中,∠ACB=90°,tanB=
如圖,Rt△ABC中,∠ACB=90°,tanB=| 3 | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,Rt△ABC中,∠C=90°,△ABC的內切圓⊙0與BC、CA、AB分別切于點D、E、F.
如圖,Rt△ABC中,∠C=90°,△ABC的內切圓⊙0與BC、CA、AB分別切于點D、E、F.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com