
【題目】如圖1所示,在A,B兩地之間有汽車站C站,客車由A地駛往C站,貨車由B地駛往A地.兩車同時出發,勻速行駛.圖2是客車、貨車離C站的路程y1 , y2(千米)與行駛時間x(小時)之間的函數關系圖象.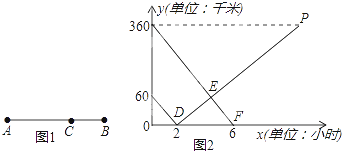
(1)填空:A,B兩地相距千米;貨車的速度是千米/時.
(2)求兩小時后,貨車離C站的路程y2與行駛時間x之間的函數表達式;
(3)客、貨兩車何時相遇?
【答案】
(1)420,30
(2)解:設2小時后,貨車離C站的路程y2與行駛時間x之間的函數表達式為y2=kx+b,根據題意得
360÷30=12(h),12+2=14(h)
∴點P的坐標為(14,360)
將點D(2,0)、點P(14,360)代入y2=kx+b中, ![]()
解得 k=30,b=﹣60
∴y2=30x﹣60
(3)解:設客車離C站的路程y1與行駛時間x之間的函數表達式為y1=k1x+b1,
根據題意得
![]()
解得k1=﹣60,b1=360
y1=﹣60x+360
由y1=y2得
30x﹣60=﹣60x+360
解得x= ![]()
答:客、貨兩車在出發后 ![]() 小時相遇.
小時相遇.
【解析】根據時間為0時,客車和貨車距離C站的距離即可解題,圖中給的函數圖像和題意可以直接得到A、B兩地的距離。
(2)根據題意和函數圖像中的數據可以得出兩個小時后,貨車離C站的路程y2與行駛時間x之間的函數關系式,一般求解函數解析式,利用待定系數法進行求解。
(3)兩個函數圖像相交,說明兩輛車相遇。根據圖中的數據分析,利用待定系數法,可求得客車離C站的路程y1與行駛時間x之間的函數解析式,然后令y1=y2,聯立得方程,即解得兩輛車相遇


科目:初中數學 來源: 題型:
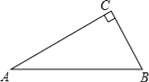
【題目】如圖,△ABC中,∠C=90°,∠A=30°.
(1)用尺規作圖作AB邊上的垂直平分線DE,交AC于點D,交AB于點E.(保留作圖痕跡,不要求寫作法和證明)
(2)連接BD,求證:DE=CD.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形AOBC,點A、B分別在x、y軸上,對角線AB、OC交于點D,點C( ![]() ,1),點M是射線OC上一動點.
,1),點M是射線OC上一動點.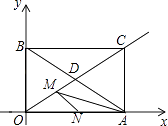
(1)求證:△ACD是等邊三角形;
(2)若△OAM是等腰三角形,求點M的坐標;
(3)若N是OA上的動點,則MA+MN是否存在最小值?若存在,請求出這個最小值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小莉的爸爸買了某演唱會的一張門票,她和哥哥兩人都很想去觀看,可門票只有一張,讀九年級的哥哥想了一個辦法,拿了八張撲克牌,將數字為1,2,3,5的四張牌給小莉,將數字為4,6,7,8的四張牌留給自己,并按如下游戲規則進行:小莉和哥哥從各自的四張牌中隨機抽出一張,然后將抽出的兩張牌數字相加,如果和為偶數,則小莉去;如果和為奇數,則哥哥去.
(1)請用樹狀圖或列表的方法表示出兩張牌數字相加和的所有可能出現的結果;
(2)哥哥設計的游戲規則公平嗎?為什么?若不公平,請設計一種公平的游戲規則.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料,并解答問題.
材料:將分式![]() 拆分成一個整式與一個分式(分子為整數)的和的形式.
拆分成一個整式與一個分式(分子為整數)的和的形式.
解:由分母為﹣x2+1,可設﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b則﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵對應任意x,上述等式均成立,∴![]() ,∴a=2,b=1
,∴a=2,b=1
∴![]() =
=![]() =
=![]() +
+![]() =x2+2+
=x2+2+![]() 這樣,分式
這樣,分式![]() 被拆分成了一個整式x2+2與一個分式
被拆分成了一個整式x2+2與一個分式![]() 的和.
的和.
解答:
(1)將分式![]() 拆分成一個整式與一個分式(分子為整數)的和的形式.
拆分成一個整式與一個分式(分子為整數)的和的形式.
(2)試說明![]() 的最小值為8.
的最小值為8.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖中顯示了10名同學平均每周用于閱讀課外書的時間和用于看電視的時間(單位:小時)。
(1)用有序實數對表示圖中各點。
(2)圖中有一個點位于方格的對角線上,這表示什么意思?
(3)圖中方格紙的對角線的左上方的點有什么共同的特點?它右下方的點呢?
(4)估計一下你每周用于閱讀課外書的時間和用于看電視的時間,在圖上描出來,這個點位于什么位置?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com