
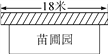
【題目】某中學課外興趣活動小組準備圍建一個矩形苗圃園,其中一邊靠墻,另外三邊用長為30米的籬笆圍成,已知墻長為18米(如圖所示),設這個苗圃園垂直于墻的一邊的長為x米.
(1)若苗圃園的面積為72平方米,求x的值;
(2)若平行于墻的一邊長不大于14米,這個苗圃園的面積有最大值和最小值嗎?如果有,求出最大值和最小值;如果沒有,請說明理由;
(3)當這個苗圃園的面積不小于100平方米時,直接寫出x的取值范圍.
【答案】(1) x=12;(2)平行于墻的一邊長為14米時,這個苗圃園的面積最大,為112平方米;(3) 6≤x≤10.
【解析】試題分析: (1)根據題意得方程求解即可,(2)設苗圃園的面積為y,根據題意得到二次函數解析式y=x(30-2x)=-2x2+30x,根據二次函數的性質求解即可,(3)由題意得不等式,即可得到結論.
試題解析:(1)根據題意得(30-2x)x=72,解得x=3或12.
∵30-2x≤18,∴x≥6,∴x=12,
(2)設苗圃園的面積為y平方米,
∴y=x(30-2x)=-2x2+30x=-2![]() +112.5,
+112.5,
由題意知30-2x≤14,∴x≥8,
由(1)知x≥6,∴x≥8.
∵-2<0,∴當x>![]() 時,y隨x的增大而減小,
時,y隨x的增大而減小,
又∵x≥8∴當x=8時,y取最大值,y最大=-2×82+30×8=112,
即平行于墻的一邊長為30-2×8=14(米)時,這個苗圃園的面積最大,為112平方米,
(3)由題意得-2x2+30x≥100,解得5≤x≤10.
由(1)知x≥6,∴6≤x≤10.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
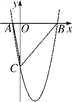
【題目】如圖,在平面直角坐標系中,已知拋物線y=ax2+bx-5與x軸交于A(-1,0),B(5,0)兩點,與y軸交于點C,連接AC,BC.
(1)求拋物線的函數表達式;
(2)若點D是y軸上的一點,且以B,C,D為頂點的三角形與△ABC相似,求點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“龜兔賽跑”是同學們熟悉的寓言故事.如圖所示,表示了寓言中的龜、兔的路程S和時間t的關系(其中直線段表示烏龜,折線段表示兔子).下列敘述正確的是( )

A. 賽跑中,兔子共休息了50分鐘
B. 烏龜在這次比賽中的平均速度是0.1米/分鐘
C. 兔子比烏龜早到達終點10分鐘
D. 烏龜追上兔子用了20分鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
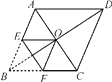
【題目】如圖,菱形ABCD的對角線相交于點O,AC=2,BD=2![]() ,將菱形按如圖方式折疊,使點B與點O重合,折痕為EF,則五邊形AEFCD的周長為_____________
,將菱形按如圖方式折疊,使點B與點O重合,折痕為EF,則五邊形AEFCD的周長為_____________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】大于1的正整數的三次方都可以分解為若干個連續奇數的和.如23=3+5,33=7+9+11,43=13+15+17+19.按此規律,若m3分解后,最后一個奇數為109,則m的值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
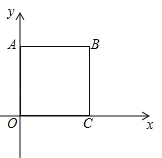
【題目】如圖,正方形OABC∽正方形ODEF,它們是以原點O為位似中心的位似圖形,位似比為1: ![]() , 點A的坐標為(0,1),則點E的坐標是________或________.
, 點A的坐標為(0,1),則點E的坐標是________或________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() .
.

(1)試說明![]() 成立的理由.(完成下面的填空)
成立的理由.(完成下面的填空)
證明:![]() ,
,
![]() ,(________________)
,(________________)
又![]() ,(已知)
,(已知)
![]() ,(________________)
,(________________)
![]() .(________________)
.(________________)
(2)若![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
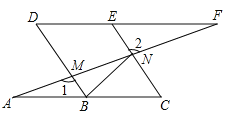
【題目】如圖,點B、E分別在AC、DF上,AF分別交BD、CE于點M、N,∠A=∠F,∠1=∠2.
(1)求證:四邊形BCED是平行四邊形;
(2)已知DE=2,連接BN,若BN平分∠DBC,求CN的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市規定了每月用水18立方米以內(含18立方米)和用水18立方米以上兩種不同的收費標準,該市的用戶每月應交水費y(元)是用水量x(立方米)的函數,其圖象如圖所示.
(1)若某月用水量為18立方米,則應交水費多少元?
(2)求當x>18時,y關于x的函數表達式,若小敏家某月交水費81元,則這個月用水量為多少立方米?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com