
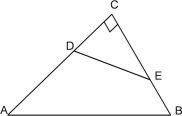
【題目】如圖,在Rt△ABC中,∠C=90°,AC=16cm,AB=20cm,動點D由點C向點A以每秒1 cm速度在邊AC上運動,動點E由點C向點B以每秒![]() cm速度在邊BC上運動,若點D,點E從點C同時出發,運動t秒(t>0),聯結DE.
cm速度在邊BC上運動,若點D,點E從點C同時出發,運動t秒(t>0),聯結DE.
(1)求證:△DCE∽△BCA.
(2)設經過點D、C、E三點的圓為⊙P.
①當⊙P與邊AB相切時,求t的值.
②在點D、點E運動過程中,若⊙P與邊AB交于點F、G(點F在點G左側),聯結CP 并延長CP交邊AB于點M,當△PFM與△CDE相似時,求t的值.

【答案】(1)見解析;(2)①![]() ;②當
;②當![]() 與
與![]() 相似時,
相似時,![]() 或
或![]() .
.
【解析】
(1)由題意得:![]() ,由
,由![]() ,
,![]() ,
,![]() 利用勾股定理求得
利用勾股定理求得![]() ,由
,由![]() ;得出
;得出![]() ,又
,又![]() ,則
,則![]() ∽
∽![]() .
.
(2)①連結![]() 并延長
并延長![]() 交
交![]() 于點
于點![]() ,利用直角三角形的斜邊中線得出
,利用直角三角形的斜邊中線得出![]() 為
為![]() 中點,
中點,![]() ,得出
,得出![]() ,利用
,利用![]() ∽
∽![]() ,得出
,得出![]() , 再利用角的等量替換得出
, 再利用角的等量替換得出![]() ,即
,即![]() ,故⊙P與邊
,故⊙P與邊![]() 相切,利用三角函數求出DE,CE即可求出t;②由題意得
相切,利用三角函數求出DE,CE即可求出t;②由題意得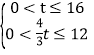 解得
解得![]() ,由①得
,由①得![]() ,
,![]() ,
,![]() ,故
,故![]() ,
,![]() ,
,![]() ,再根據相似三角形分情況討論即可求解.
,再根據相似三角形分情況討論即可求解.
(1)證明:由題意得:![]() ,∵
,∵![]() ,
,![]() ,
,![]() ;
;
∴![]() ,∵
,∵![]() ;
;
∴![]()
又∵![]()
∴![]() ∽
∽![]() .
.
(2)①連結![]() 并延長
并延長![]() 交
交![]() 于點
于點![]() ,
,

∵![]() ,
,
∴DE是⊙![]() 的直徑
的直徑
即![]() 為
為![]() 中點,
中點,
∴![]() .
.
∴![]() ,∵
,∵![]() ∽
∽![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]()
∴![]() ;
;
∵⊙P與邊![]() 相切,
相切,
∴點![]() 為切點,
為切點, ![]() 為⊙
為⊙![]() 的直徑,
的直徑,
∵![]() 解得
解得![]() ,∴
,∴![]()
![]() 得
得![]() 即
即![]() .
.
②由題意得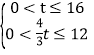 解得
解得![]() ,由①得
,由①得![]() ,
,![]() ,
,![]()
∴,
![]() ,
,![]() ,
,
∵![]()
∴由![]() 與
與![]() 相似可得:
相似可得:
情況一:![]() 得
得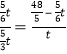 解得:
解得:![]() ; 0<
; 0<![]() ≤9
≤9
情況二:![]() 得
得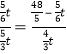 解得:
解得:![]() ; 0<
; 0<![]() ≤9
≤9
∴綜上所述:當![]() 與
與![]() 相似時.
相似時. ![]() 或
或![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,RtΔABC中,AB=AC,D、E是斜邊BC上兩點,∠DAE=45°,將ΔADC繞點A順時針旋轉90°后,得到ΔAFB,連接EF,下列結論:①ΔAED≌ΔAEF,②![]() ,③ΔABC的面積等于四邊形AFBD的面積,④
,③ΔABC的面積等于四邊形AFBD的面積,④![]() ,⑤BE+DC=DE,其中正確的是( )
,⑤BE+DC=DE,其中正確的是( )
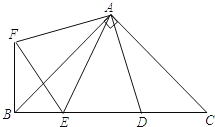
A. ①②④B. ①③④C. ③④⑤D. ①③⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的最大值為4,且該拋物線與
的最大值為4,且該拋物線與![]() 軸的交點為
軸的交點為![]() ,頂點為
,頂點為![]() .
.
(1)求該二次函數的解析式及點![]() ,
,![]() 的坐標;
的坐標;
(2)點![]() 是
是![]() 軸上的動點,
軸上的動點,
①求![]() 的最大值及對應的點
的最大值及對應的點![]() 的坐標;
的坐標;
②設![]() 是
是![]() 軸上的動點,若線段
軸上的動點,若線段![]() 與函數
與函數![]() 的圖像只有一個公共點,求
的圖像只有一個公共點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() (
(![]() >0)與
>0)與![]() 軸交于A,B兩點(A點在B點的左邊),與
軸交于A,B兩點(A點在B點的左邊),與![]() 軸交于點C。
軸交于點C。
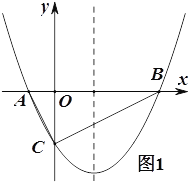
(1)如圖1,若△ABC為直角三角形,求![]() 的值;
的值;
(2)如圖1,在(1)的條件下,點P在拋物線上,點Q在拋物線的對稱軸上,若以BC為邊,以點B,C,P,Q為頂點的四邊形是平行四邊形,求P點的坐標;
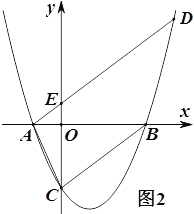
(3)如圖2,過點A作直線BC的平行線交拋物線于另一點D,交![]() 軸交于點E,若AE:ED=1:4,求
軸交于點E,若AE:ED=1:4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
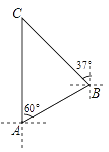
【題目】知識改變世界,科技改變生活.導航裝備的不斷更新極大方便了人們的出行.如圖,某校組織學生乘車到黑龍灘(用C表示)開展社會實踐活動,車到達A地后,發現C地恰好在A地的正北方向,且距離A地13千米,導航顯示車輛應沿北偏東60°方向行駛至B地,再沿北偏西37°方向行駛一段距離才能到達C地,求B、C兩地的距離.(參考數據:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】知識背景
當a>0且x>0時,因為(![]() ﹣
﹣![]() )2≥0,所以x﹣2
)2≥0,所以x﹣2![]() +
+![]() ≥0,從而x+
≥0,從而x+![]() (當x=
(當x=![]() 時取等號).
時取等號).
設函數y=x+![]() (a>0,x>0),由上述結論可知:當x=
(a>0,x>0),由上述結論可知:當x=![]() 時,該函數有最小值為2
時,該函數有最小值為2![]() .
.
應用舉例
已知函數為y1=x(x>0)與函數y2=![]() (x>0),則當x=
(x>0),則當x=![]() =2時,y1+y2=x+
=2時,y1+y2=x+![]() 有最小值為2
有最小值為2![]() =4.
=4.
解決問題
(1)已知函數為y1=x+3(x>﹣3)與函數y2=(x+3)2+9(x>﹣3),當x取何值時,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某設備租賃使用成本包含以下三部分:一是設備的安裝調試費用,共490元;二是設備的租賃使用費用,每天200元;三是設備的折舊費用,它與使用天數的平方成正比,比例系數為0.001.若設該設備的租賃使用天數為x天,則當x取何值時,該設備平均每天的租貨使用成本最低?最低是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD 中,對角線AC,BD交于點O,以 AD,OD為鄰邊作平行四邊形ADOE,連接BE.
(1) 求證:四邊形AOBE是菱形;
(2) 若∠EAO+∠DCO=180°,DC=2,求四邊形ADOE的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com