【題目】有如下說法：①直線是一個平角；②如果線段AB＝BC，則B是線段AC的中點；③射線AB與射線BA表示同一射線；④用一個擴大2倍的放大鏡去看一個角，這個角擴大2倍；⑤兩點之間，直線最短；⑥120.5°＝120°30′，其中正確的有（ ）
A.1個B.2個C.3個D.4個
科目：初中數學 來源： 題型：
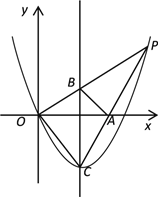
【題目】如圖，已知拋物線y=ax2+bx的頂點為C（1，
），P是拋物線上位于第一象限內的一點，直線OP交該拋物線對稱軸于點B，直線CP交x軸于點A．
（1）求該拋物線的表達式；
（2）如果點P的橫坐標為m，試用m的代數式表示線段BC的長；
（3）如果△ABP的面積等于△ABC的面積，求點P坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】剛剛升入初一，學習成績優異但體育一般的王晴同學未雨綢繆，已經為將來的體育中考做起了準備.上周末她在家練習1分鐘跳繩，以每分鐘150下為基準，超過或不足的部分分別用正負數來表示，8次成績（單位：下）分別是－10，－8，－5，－2，＋2，＋8，＋3，－4.
（1）成績最好的一次比最差的一次多跳多少下？
（2）求王晴這8次跳繩的平均成績.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，甲、乙兩人以相同路線前往離學校12千米的地方參加植樹活動．分析甲、乙兩人前往目的地所行駛的路程S（千米）隨時間t（分鐘）變化的函數圖象，解決下列問題：
（1）求出甲、乙兩人所行駛的路程S甲、S乙與t之間的關系式；
（2）甲行駛15分鐘后，甲、乙兩人相距多少千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
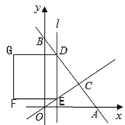
【題目】如圖，直線
分別于
軸、
軸交于A、B兩點，與直線
交于點C(2,4)，平行于軸的直線
從原點
出發，以每秒1個單位長度的速度沿軸向右平移，直線分別交直線AB、直線OC于點D、E，以DE為邊向左側作正方形DEFG，當直線經過點A時停止運動，設直線的運動時間為
(秒).
(1)
(2)設線段DE的長度為
求
與之間的函數關系式；
(3)當正方形DEFG的邊GF落在軸上，求出的值；
(4)當
時，若正方形DEFG和△OCB重疊部分面積為4，則的值為________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明同學為了解自己居住的小區家庭生活用水情況，從中隨機調查了其中
的家庭一年的月平均用水量（單位：頓）.并將調查結果制成了如圖所示的條形和扇形統計圖.
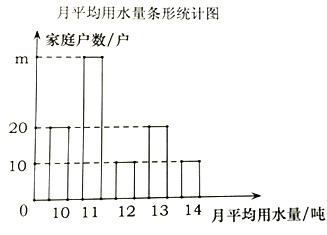
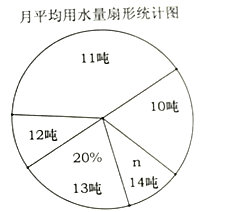
小明隨機調查了 戶家庭，該小區共有 戶家庭；
，
；
這個樣本數據的眾數是 ，中位數是 ；
根據樣本數據，請估計該小區家庭月平均用水量不超過
噸的有多少戶？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠B＝∠C＝36°，AB的垂直平分線交BC于點D，交AB于點H，AC的垂直平分線交BC于點E，交AC于點G，連接AD，AE，則下列結論錯誤的是( )
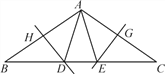
A. 
B. AD，AE將∠BAC三等分
C. △ABE≌△ACD D. S△ADH＝S△CEG
【答案】A
【解析】試題解析：∵∠B=∠C=36°，∴AB=AC，∠BAC=108°，∵DH垂直平分AB，EG垂直平分AC，∴DB=DA，EA=EC，∴∠B=∠DAB=∠C=∠CAE=36°，∴△BDA∽△BAC，∴
，又∵∠ADC=∠B+∠BAD=72°，∠DAC=∠BAC﹣∠BAD=72°，∴∠ADC=∠DAC，∴CD=CA=BA，∴BD=BC﹣CD=BC﹣AB，則
=
，即=，故A錯誤；
∵∠BAC=108°，∠B=∠DAB=∠C=∠CAE=36°，∴∠DAE=∠BAC﹣∠DAB﹣∠CAE=36°，即∠DAB=∠DAE=∠CAE=36°，∴AD，AE將∠BAC三等分，故B正確；
∵∠BAE=∠BAD+∠DAE=72°，∠CAD=∠CAE+∠DAE=72°，∴∠BAE=∠CAD，在△BAE和△CAD中，∵∠B=∠C，AB=AC，∠BAE=∠CAD，∴△BAE≌△CAD，故C正確；
由△BAE≌△CAD可得S△BAE=S△CAD，即S△BAD+S△ADE=S△CAE+S△ADE，∴S△BAD=S△CAE，又∵DH垂直平分AB，EG垂直平分AC，∴S△ADH=
S△ABD，S△CEG=S△CAE，∴S△ADH=S△CEG，故D正確．
故選A．
【題型】單選題
【結束】
11
【題目】紅細胞是人體中血液運輸氧氣的主要媒介，人體中紅細胞的直徑約為0．0000077m，將0．0000077用科學記數法表示為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
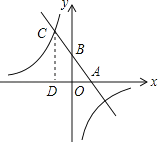
【題目】已知，如圖，一次函數y=kx+b（k、b為常數，k≠0）的圖象與x軸、y軸分別交于A、B兩點，且與反比例函數y=
（n為常數且n≠0）的圖象在第二象限交于點C．CD⊥x軸，垂直為D，若OB=2OA=3OD=6．
（1）求一次函數與反比例函數的解析式；
（2）求兩函數圖象的另一個交點坐標；
（3）直接寫出不等式；kx+b≤
的解集．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，二次函數y=ax2+bx+c的圖象開口向上，圖象經過點（﹣1，2）和（1，0），且與y軸交于負半軸，給出六個結論：①a＞0；②b＞0；③c＞0；④a+b+c=0；⑤b2﹣4ac＞0；⑥2a﹣b＞0，其中正確結論序號是_____．
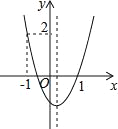
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
