
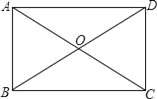
【題目】如圖,ABCD的對角線AC,BD相交于點O,△OAB是等邊三角形.
(1)求證:ABCD為矩形;
(2)若AB=4,求ABCD的面積.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,![]() 為平行四邊形
為平行四邊形![]() 的對角線,
的對角線,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 、
、![]() 相交于
相交于![]() ,直線
,直線![]() 交線段
交線段![]() 的延長線于
的延長線于![]() ,下面結論:①
,下面結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 其中正確的個數是( )
其中正確的個數是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
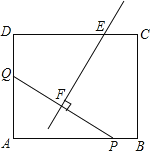
【題目】如圖,在矩形ABCD中,AB=12,AD=10.點Q從點D出發沿DA以每秒1個單位長度的速度向點A勻速運動;點P從點A出發沿AB以每秒2個單位長度的速度向點B勻速運動.伴隨P、Q的運動,直線EF保持垂直平分PQ于點F,交射線DC于點E,點P、Q同時出發,當點P到達B點時停止運動,點Q也隨之停止.設點P運動時間為t秒(0<t<6),t=____________時,EF能平分矩形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的文字,解答問題:大家知道![]() 是無理數,而無理數是無限不循環小數,因此
是無理數,而無理數是無限不循環小數,因此![]() 的小數部分我們不可能全部地寫出來,于是小明用
的小數部分我們不可能全部地寫出來,于是小明用![]() -1來表示
-1來表示![]() 的小數部分,事實上,小明的表示方法是有道理的,因為
的小數部分,事實上,小明的表示方法是有道理的,因為![]() <
<![]() <
<![]() ,所以
,所以![]() 的整數部分是1,將這個數減去其整數部分,差就是小數部分.請據此解答:
的整數部分是1,將這個數減去其整數部分,差就是小數部分.請據此解答:
(1)![]() 的整數部分是 ,小數部分是 .
的整數部分是 ,小數部分是 .
(2)如果![]() 的小數部分為a,
的小數部分為a,![]() 的整數部分為b,求a+b-
的整數部分為b,求a+b-![]() 的值;
的值;
(3)若設2+![]() 的整數部分為x,小數部分為y,求(y-x)2的值.
的整數部分為x,小數部分為y,求(y-x)2的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,(1)正方形ABCD及等腰Rt△AEF有公共頂點A,∠EAF=90°, 連接BE、DF.將Rt△AEF繞點A旋轉,在旋轉過程中,BE、DF具有怎樣的數量關系和位置關系?結合圖(1)給予證明;
(2)將(1)中的正方形ABCD變為矩形ABCD,等腰Rt△AEF變為Rt△AEF,且AD=kAB,AF=kAE,其他條件不變.(1)中的結論是否發生變化?結合圖(2)說明理由;
(3)將(2)中的矩形ABCD變為平行四邊形ABCD,將Rt△AEF變為△AEF,且∠BAD=∠EAF=![]() ,其他條件不變.(2)中的結論是否發生變化?結合圖(3),如果不變,直接寫出結論;如果變化,直接用k表示出線段BE、DF的數量關系,用
,其他條件不變.(2)中的結論是否發生變化?結合圖(3),如果不變,直接寫出結論;如果變化,直接用k表示出線段BE、DF的數量關系,用![]() 表示出直線BE、DF形成的銳角
表示出直線BE、DF形成的銳角![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是等邊三角形ABC內一點,將線段AD繞點A順時針旋轉60°,得到線段AE,連接CD,BE.
(1)求證:∠AEB=∠ADC;
(2)連接DE,若∠ADC=105°,求∠BED的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y![]() xb與x軸交于點A,與y軸交于點B,與直線y=x交于點E,點E的橫坐標為3.
xb與x軸交于點A,與y軸交于點B,與直線y=x交于點E,點E的橫坐標為3.
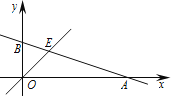
(1)求點A的坐標.
(2)在x軸上有一點P(m,0),過點P作x軸的垂線,與直線y![]() xb交于點C,與直線y=x交于點D.若CD≥5,求m的取值范圍.
xb交于點C,與直線y=x交于點D.若CD≥5,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象交于A、B兩點,點A坐標為
的圖象交于A、B兩點,點A坐標為![]() ,點B坐標為
,點B坐標為![]() ,OA與x軸正半軸夾角的正切值為
,OA與x軸正半軸夾角的正切值為![]() ,直線AB交y軸于點C,過C作y軸的垂線,交反比例函數圖象于點D,連接OD、BD.
,直線AB交y軸于點C,過C作y軸的垂線,交反比例函數圖象于點D,連接OD、BD.
(1)求一次函數與反比例函數的解析式;
(2)連接BD,求出BDC的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,點O在邊AB上,以點O為圓心,OA為半徑的圓經過點C,過點C作直線MN,使∠BCM=2∠A.
(1)判斷直線MN與⊙O的位置關系,并說明理由;
(2)若OA=4,∠BCM=60°,求圖中陰影部分的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com