
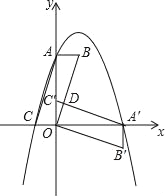
【題目】如圖,在平面直角坐標系中,平行四邊形ABOC如圖放置,將此平行四邊形繞點O順時針旋轉90°得到平行四邊形A′B′OC′.拋物線y=﹣x2+2x+3經過點A、C、A′三點.
(1)求A、A′、C三點的坐標;
(2)求平行四邊形ABOC和平行四邊形A′B′OC′重疊部分△C′OD的面積;
(3)點M是第一象限內拋物線上的一動點,問點M在何處時,△AMA′的面積最大?最大面積是多少?并寫出此時M的坐標.
【答案】(1)C(﹣1,0),A′(3,0),A(0,3);(2)![]() ;(3)S△AMA′==﹣
;(3)S△AMA′==﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,∴當m=
,∴當m=![]() 時,S△AMA'的值最大,最大值為
時,S△AMA'的值最大,最大值為![]() ,此時M點坐標為(
,此時M點坐標為(![]() ,
,![]() ).
).
【解析】
(1)利用拋物線與x軸的交點問題可求出C(﹣1,0),A′(3,0);計算自變量為0時的函數值可得到A(0,3);
(2)先由平行四邊形的性質得AB∥OC,AB=OC,易得B(1,3),根據勾股定理和三角形面積公式得到OB=![]() ,S△AOB=
,S△AOB=![]() ,再根據旋轉的性質得∠ACO=∠OC′D,OC′=OC=1,接著證明△C′OD∽△BOA,利用相似三角形的性質得
,再根據旋轉的性質得∠ACO=∠OC′D,OC′=OC=1,接著證明△C′OD∽△BOA,利用相似三角形的性質得![]() =(
=(![]() )2,則可計算出S△C′OD;
)2,則可計算出S△C′OD;
(3)根據二次函數圖象上點的坐標特征,設M點的坐標為(m,﹣m2+2m+3),0<m<3,作MN∥y軸交直線AA′于N,求出直線AA′的解析式為y=﹣x+3,則N(m,﹣m+3),于是可計算出MN=﹣m2+3m,再利用S△AMA′=S△ANM+S△MNA′和三角形面積公式得到S△AMA′=﹣![]() m2+
m2+![]() m,然后根據二次函數的最值問題求出△AMA′的面積最大值,同時即可確定此時M點的坐標.
m,然后根據二次函數的最值問題求出△AMA′的面積最大值,同時即可確定此時M點的坐標.
(1)當y=0時,﹣x2+2x+3=0,
解得x1=3,x2=﹣1,
則C(﹣1,0),A′(3,0),
當x=0時,y=3,則A(0,3);
(2)∵四邊形ABOC為平行四邊形,
∴AB∥OC,AB=OC,
而C(﹣1,0),A(0,3),
∴B(1,3),
∴OB=![]() =
=![]() ,S△AOB=
,S△AOB=![]() ×3×1=
×3×1=![]() ,
,
又∵平行四邊形ABOC旋轉90°得平行四邊形A′B′OC′,
∴∠ACO=∠OC′D,OC′=OC=1,
又∵∠ACO=∠ABO,
∴∠ABO=∠OC′D.
又∵∠C′OD=∠AOB,
∴△C′OD∽△BOA,
∴![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() ,
,
∴S△C′OD=![]() ×
×![]() =
=![]() ;
;
(3)設M點的坐標為(m,﹣m2+2m+3),0<m<3,
作MN∥y軸交直線AA′于N,易得直線AA′的解析式為y=﹣x+3,則N(m,﹣m+3),
∵MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,
∴S△AMA′=S△ANM+S△MNA′
=![]() MN3
MN3
=![]() (﹣m2+3m)
(﹣m2+3m)
=﹣![]() m2+
m2+![]() m
m
=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∴當m=![]() 時,S△AMA'的值最大,最大值為
時,S△AMA'的值最大,最大值為![]() ,此時M點坐標為(
,此時M點坐標為(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
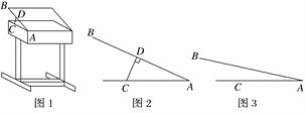
【題目】某課桌生產廠家研究發現,傾斜12°~24°的桌面有利于學生保持軀體自然姿勢.根據這一研究,廠家決定將水平桌面做成可調節角度的桌面.新桌面的設計圖如圖1,AB可繞點A旋轉,在點C處安裝一根可旋轉的支撐臂CD,AC=30 cm.
(1)如圖2,當∠BAC=24°時,CD⊥AB,求支撐臂CD的長;
(2)如圖3,當∠BAC=12°時,求AD的長.(結果保留根號)
(參考數據:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中數學 來源: 題型:
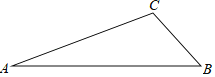
【題目】如圖,在△ABC紙板中,AC=4,BC=2,AB=5,P是AC上一點,過點P沿直線剪下一個與△ABC相似的小三角形紙板,如果有4種不同的剪法,那么AP長的取值范圍是__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】結果如此巧合!
下面是小穎對一道題目的解答.
題目:如圖,Rt△ABC的內切圓與斜邊AB相切于點D,AD=3,BD=4,求△ABC的面積.
解:設△ABC的內切圓分別與AC、BC相切于點E、F,CE的長為x.
根據切線長定理,得AE=AD=3,BF=BD=4,CF=CE=x.
根據勾股定理,得(x+3)2+(x+4)2=(3+4)2.
整理,得x2+7x=12.
所以S△ABC=![]() ACBC
ACBC
=![]() (x+3)(x+4)
(x+3)(x+4)
=![]() (x2+7x+12)
(x2+7x+12)
=![]() ×(12+12)
×(12+12)
=12.
小穎發現12恰好就是3×4,即△ABC的面積等于AD與BD的積.這僅僅是巧合嗎?
請你幫她完成下面的探索.
已知:△ABC的內切圓與AB相切于點D,AD=m,BD=n.
可以一般化嗎?
(1)若∠C=90°,求證:△ABC的面積等于mn.
倒過來思考呢?
(2)若ACBC=2mn,求證∠C=90°.
改變一下條件……
(3)若∠C=60°,用m、n表示△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
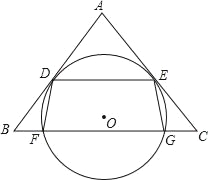
【題目】如圖,O是△ABC內一點,⊙O與BC相交于F、G兩點,且與AB、AC分別相切于點D、E,DE∥BC.連接 DF、EG.
(1)求證:AB=AC.
(2)已知 AB=5,BC=6.求四邊形DFGE是矩形時⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點 O 是△ABC 的邊 AB 上一點,以 OB 為半徑的⊙O 交 BC 于點 D,過點 D 的切線交 AC 于點 E,且 DE⊥AC.
(1)證明:AB=AC;
(2)設 AB=![]() cm,BC=2cm,當點 O 在 AB 上移動到使⊙O 與邊 AC 所在直線相切時, 求⊙O 的半徑.
cm,BC=2cm,當點 O 在 AB 上移動到使⊙O 與邊 AC 所在直線相切時, 求⊙O 的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把球放在長方體紙盒內,球的一部分露出盒外,其截面如圖所示,已知EF=CD=4 cm,則球的半徑長是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中數學 來源: 題型:
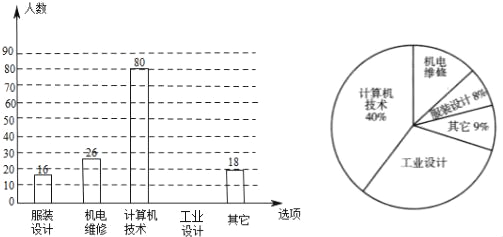
【題目】每年5月的第二周為“職業教育活動周”,今年我省開展了以“弘揚工匠精神,打造技能強國”為主題的系列活動.活動期間某職業中學組織全校師生并邀請學生家長和社區居民參加“職教體驗觀摩”活動,相關職業技術人員進行了現場演示,活動后該校教務處隨機抽取了部分學生進行調查:“你最感興趣的一種職業技能是什么?”并對此進行了統計,繪制了統計圖(均不完整).請解答以下問題:
(1)補全條形統計圖和扇形統計圖;
(2)若該校共有1800名學生,請估計該校對“工業設計”最感興趣的學生有多少人?
(3)要從這些被調查的學生中,隨機抽取一人進行訪談,那么正好抽到對“機電維修”最感興趣的學生的概率是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com