Question

【題目】如圖1，點O為直線AB上一點，過點O作射線OC，使∠BOC=120°，將一直角三角形的直角（∠MON=90°）頂點放在點O處，一邊OM在射線OB上，另一邊ON在直線AB的下方．

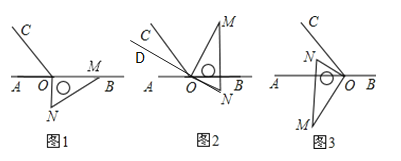
（1）在圖1中，∠NOC= ．

（2）將圖1中的三角板繞點O逆時針旋轉至圖2，使一邊OM在∠BOC的內部，且恰好平分∠BOC，問：NO的延長線OD是否平分∠AOC？請說明理由；

（3）將圖1中的三角板繞點O按每秒6°的速度沿逆時針方向旋轉一周，在旋轉的過程中，第t秒時，直線ON恰好平分銳角∠AOC，則t的值為 秒？（直接寫出結果）

（4）將圖1中的三角板繞點O旋轉至圖3的位置，使ON在∠AOC的內部，則∠AOM-∠NOC= °

Answer 1

【答案】（1）150°；（2）平分，理由詳見解析；（3）或；（4）30

【解析】

（1）根據的度數求出的度數，然后利用即可求解；

（2）根據角平分線的定義求出，進而求出，則有

，則說明平分；

（3）根據第（2）問可知圖2時直線ON平分銳角，求出的度數即可求出時間；另一種情況是ON轉到的內部平分，求出此時相對于第一種情況又轉過了多少度，經過了多長時間即可得出最后的結果；

（4）根據的度數表示出的度數，然后利用即可求解．

解:

平分．理由如下:

平分

，

，

平分；

由可知，當時，直線平分銳角，此時；

另外一種情況是ON轉到的內部平分，即相對于圖（2）時ON又轉過 ，所以又過了 ，所以當ON再次平分銳角時，

直線ON恰好平分銳角∠AOC時，或秒．

（4）