
【題目】某天上午7:30,小芳在家通過滴滴打車軟件打車前往動車站搭乘當天上午8:30的動車.記汽車的行駛時間為t小時,行駛速度為v千米/小時(汽車行駛速度不超過60千米/小時).根據經驗,v,t的一組對應值如下表:
V(千米/小時) | 20 | 30 | 40 | 50 | 60 |
T(小時) | 0.6 | 0.4 | 0.3 | 0.25 | 0.2 |
(1)根據表中的數據描點,求出平均速度v(千米/小時)關于行駛時間t(小時)的函數表達式;
(2)若小芳從開始打車到上車用了10分鐘,小芳想在動車出發前半小時到達動車站,若汽車的平均速度為32千米/小時,小芳能否在預定的時間內到達動車站?請說明理由;
(3)若汽車到達動車站的行駛時間t滿足0.3<t<0.5,求平均速度v的取值范圍.

【答案】(1)v=![]() ;(2)若汽車的平均速度為32千米/小時,小芳不能在預定的時間內到達動車站;(3)平均速度v的取值范圍是24<v<40
;(2)若汽車的平均速度為32千米/小時,小芳不能在預定的時間內到達動車站;(3)平均速度v的取值范圍是24<v<40
【解析】
(1)根據表格中數據,可知v是t的反比例函數,設v=![]() ,利用待定系數法求出k即可;
,利用待定系數法求出k即可;
(2)根據時間t=![]() 小時,求出速度,即可判斷;
小時,求出速度,即可判斷;
(3)根據自變量的取值范圍,求出函數值的取值范圍即可.
(1)根據表格中數據,可知v=![]() ,
,
∵v=20時,t=0.6,
∴k=20×0.6=12,
∴v=![]() (t≥0.2).
(t≥0.2).
(2)∵1﹣![]() -
-![]() =
=![]() ,
,
∴t=![]() 時,v=
時,v=![]() =36>32,
=36>32,
∴若汽車的平均速度為32千米/小時,小芳不能在預定的時間內到達動車站;
(3)∵0.3<t<0.5,
∴24<v<40,
答:平均速度v的取值范圍是24<v<40.


科目:初中數學 來源: 題型:
【題目】如圖,已知等腰三角形ABC的底角為30°,以BC為直徑的⊙O與底邊AB交于點D,過D作DE⊥AC,垂足為E.
(1)證明:DE為⊙O的切線;
(2)若BC=4,求陰影部分的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
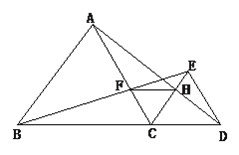
【題目】如圖,已知點B、C、D在同一條直線上,△ABC和△CDE都是等邊三角形.BE交AC于F,AD交CE于H,
①求證:△BCE≌△ACD;
②求證:CF=CH;
③判斷△CFH的形狀并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
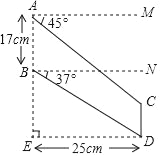
【題目】“C919”大型客機首飛成功,激發了同學們對航空科技的興趣,如圖是某校航模興趣小組獲得的一張數據不完整的航模飛機機翼圖紙,圖中AB∥CD,AM∥BN∥ED,AE⊥DE,請根據圖中數據,求出線段BE和CD的長.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,結果保留小數點后一位)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB⊥BC,DC⊥BC,E是BC上一點,使得AE⊥DE;
(1)求證:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的長;
(3)當△AED∽△ECD時,請寫出線段AD、AB、CD之間數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=CB,O是AB的中點,CA與⊙O相切于點E,CO交⊙O于點D
(1)求證:CB是⊙O的切線;
(2)若∠ACB=80°,點P是⊙O上一個動點(不與D,E兩點重合),求∠DPE的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,直線y1=x+1在平面直角坐標系xOy中.

(1)在平面直角坐標系xOy中畫出y2=﹣2x+4的圖象;
(2)求y1與y2的交點坐標;
(3)根據圖象直接寫出當y1≥y2時,x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角坐標系中,⊙M經過原點O(0,0),點A(![]() ,0)與點B(0,﹣1),點D在劣弧OA上,連接BD交x軸于點C,且∠COD=∠CBO.
,0)與點B(0,﹣1),點D在劣弧OA上,連接BD交x軸于點C,且∠COD=∠CBO.
(1)請直接寫出⊙M的直徑,并求證BD平分∠ABO;
(2)在線段BD的延長線上尋找一點E,使得直線AE恰好與⊙M相切,求此時點E的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com