
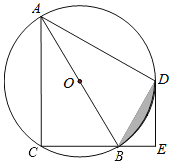
【題目】如圖,四邊形ACBD是⊙O的內接四邊形,AB為直徑,弧CD=弧AD,DE⊥BC,垂足為E.
(1)求證:BD平分∠ABE;
(2)判斷直線ED與⊙O的位置關系,并說明理由;
(3)若BE=2,AB=8,求陰影部分的面積.
【答案】(1)見解析;(2)直線DE與圓O相切,理由見解析;(3)陰影部分的面積=![]() π-
π-![]() .
.
【解析】
(1)根據圓周角定理,由弧CD=弧AD,得到∠CAD=∠ABD,再根據圓內接四邊形的性質得∠DBE=∠CAD,所以∠ABD=∠DBE;
(2)連結OD,如圖,利用內錯角相等證明OD∥CE,而DE⊥BC,則OD⊥DE,于是根據切線的判定定理可得DE為⊙O的切線;
(3)利用扇形面積公式、等邊三角形的面積公式和陰影部分的面積解答即可.
證明:(1)∵弧CD=弧AD,
∴∠CAD=∠ABD,
∵∠DBE=∠CAD,
∴∠ABD=∠DBE.
即BD平分∠ABE
(2)直線DE與圓O相切,理由如下:
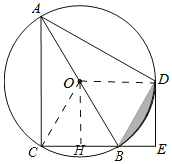
連結OD,OC,如圖,
∵OB=OD,
∴∠OBD=∠ODB,
而∠OBD=∠DBE,
∴∠ODB=∠DBE,
∴OD∥CE,
∵DE⊥BC,
∴OD⊥DE,
∴DE為⊙O的切線
(3)作OH⊥BC于H,則四邊形ODEH為矩形,
∴OD=EH,
∵BE=2,AB=8,
∴OB=OD=BD=4,
∴在Rt△DBE中,∠BDE=30°,
∴DE=2![]() ,
,
∴陰影部分的面積=![]() π-
π-![]() .
.


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,點
中,點![]() 在邊
在邊![]() 上,且
上,且![]() ,
,![]() ,過點
,過點![]() 作
作![]() ,交邊
,交邊![]() 于點
于點![]() ,將
,將![]() 沿著
沿著![]() 折疊,得
折疊,得![]() ,與邊
,與邊![]() 分別交于點
分別交于點![]() ,
,![]() .若
.若![]() 的面積為15,則
的面積為15,則![]() 的面積是( )
的面積是( )
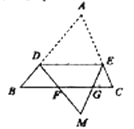
A. 0.5B. 0.6C. 0.8D. 1.2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A在反比例函數y=![]() (x>0)的圖像上,點B在反比例函數y=
(x>0)的圖像上,點B在反比例函數y=![]() (x>0)的圖像上,AB∥x軸,BC⊥x軸,垂足為C,連接AC,若△ABC的面積是6,則k的值為( )
(x>0)的圖像上,AB∥x軸,BC⊥x軸,垂足為C,連接AC,若△ABC的面積是6,則k的值為( )

A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
科目:初中數學 來源: 題型:
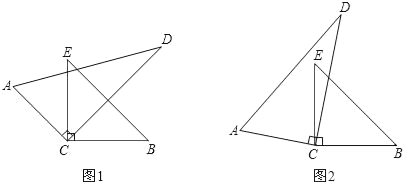
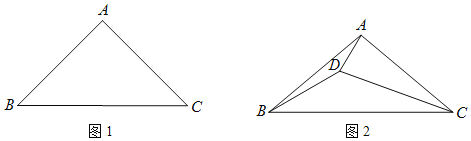
【題目】如圖,將一副直角三角形的直角頂點C疊放一起
(1)如圖1,若CE恰好是∠ACD的角平分線,請你猜想此時CD是不是的∠ECB的角平分線?并簡述理由;
(2)如圖1,若∠ECD=α,CD在∠ECB的內部,請猜想∠ACE與∠DCB是否相等?并簡述理由;
(3)在如圖2的條件下,請問∠ECD與∠ACB的和是多少?并簡述理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
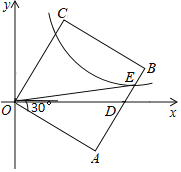
【題目】如圖,矩形OABC的邊AB與x軸交于點D,與反比例函數y=![]() (k>0)在第一象限的圖象交于點E,∠AOD=30°,點E的縱坐標為1,△ODE的面積是
(k>0)在第一象限的圖象交于點E,∠AOD=30°,點E的縱坐標為1,△ODE的面積是![]() ,則k的值是( )
,則k的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
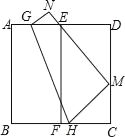
【題目】如圖,將邊長為3的正方形紙片ABCD對折,使AB與DC重合,折痕為EF,展平后,再將點B折到邊CD上,使邊AB經過點E,折痕為GH,點B的對應點為M,點A的對應點為N,那么折痕GH的長為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
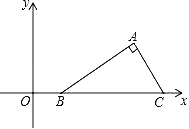
【題目】如圖,在平面直角坐標系中Rt△ABC的斜邊BC在x軸上,點B坐標為(1,0),AC=2,∠ABC=30°,把Rt△ABC先繞B點順時針旋轉180°,然后再向下平移2個單位,則A點的對應點A′的坐標為( )
A. (﹣4,﹣2﹣![]() ) B. (﹣4,﹣2+
) B. (﹣4,﹣2+![]() ) C. (﹣2,﹣2+
) C. (﹣2,﹣2+![]() ) D. (﹣2,﹣2﹣
) D. (﹣2,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
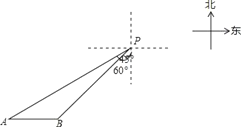
【題目】一艘輪船位于燈塔P南偏西60°方向,距離燈塔20海里的A處,它向東航行多少海里到達燈塔P南偏西45°方向上的B處(參考數據:![]() ≈1.732,結果精確到0.1)?
≈1.732,結果精確到0.1)?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,將線段AC繞著點C逆時針旋轉得到線段CD,旋轉角為α.
(1)如圖,∠BAC=90°,α=45°,試求點D到邊AB,AC的距離的比值;
(2)如圖,∠BAC=100°,α=20°,連接AD,BD,求∠CBD的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com