
【題目】如圖1,在銳角△ABC中,AD⊥BC于D,BE⊥AC于E,AD與BE相交于F,且BF=AC。求證:ED平分∠FEC。

【答案】證明見解析
【解析】分析:求出∠DBF=∠DAC,由AAS證明△BDF≌△ADC.得出對應邊相等BD=AD,由等腰直角三角形的性質得出∠BAD=∠ABD=45°,證明A、B、D、E四點共圓,由圓周角定理得出∠BED=∠BAD=45°,得出∠CED=∠BED,即可得出結論.
本題解析:
∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=90°,∠AEB=∠FEC=90°,
∵∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,
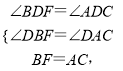
∴△BDF≌△ADC(AAS),
∴BD=AD,
∴∠BAD=∠ABD=45°,
∵∠AEB=∠ADB=90°,
∴A、B、D、E四點共圓,
∴∠BED=∠BAD=45°,
∴∠CED=90°-45°=45°=∠BED,
∴ED平分∠FEC。


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:初中數學 來源: 題型:
【題目】學生的學業負擔過重會嚴重影響學生對待學習的態度.為此我市教育部門對部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:對學習很感興趣;對學習較感興趣;對學習不感興趣),并將調查結果繪制成圖①和圖②的統計圖(不完整).請根據圖中提供的信息,解答下列問題:
(1)此次抽樣調查中,共調查了名學生;
(2)將圖①補充完整;
(3)求出圖②中C級所占的圓心角的度數;
(4)根據抽樣調查結果,請你估計我市近8000名八年級學生中大約有多少名學生學習態度達標(達標包括A級和B級)?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司保安部計劃從商店購買同一品牌的應急燈和手電筒,已知購買一個應急燈比購買一個手電筒多用![]() 元,若用
元,若用![]() 元購買應急燈和用
元購買應急燈和用![]() 元購買手電筒,則購買應急燈的個數是購買手電筒個數的一半.
元購買手電筒,則購買應急燈的個數是購買手電筒個數的一半.
(1)分別求出該品牌應急燈、手電筒的定價;
(2)經商談,商店給予該公司購買一個該品牌應急燈贈送一個該品牌手電筒的優惠,如果該公司需要手電筒的個數是應急燈個數的![]() 倍還多
倍還多![]() 個,且該公司購買應急燈和手電筒的總費用不超過
個,且該公司購買應急燈和手電筒的總費用不超過![]() 元,那么該公司最多可購買多少個該品牌應急燈?
元,那么該公司最多可購買多少個該品牌應急燈?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與直線
與直線![]() :
:![]() 交于點
交于點![]() ,點
,點![]() 的橫坐標為
的橫坐標為![]() ,直線
,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,將直線
,將直線![]() 向上平移后得到直線
向上平移后得到直線![]() ,直線
,直線![]() 剛好經過拋物線與
剛好經過拋物線與![]() 軸正半軸的交點
軸正半軸的交點![]() 和與
和與![]() 軸的交點
軸的交點![]() .
.

(1)直接寫出點![]() 和點
和點![]() 的坐標,并求出點
的坐標,并求出點![]() 的坐標;
的坐標;
(2)若點![]() 是拋物線第一象限內的一個動點,連接
是拋物線第一象限內的一個動點,連接![]() ,交直線
,交直線![]() 于點
于點![]() ,連接
,連接![]() 和
和![]() .設
.設![]() 的面積為
的面積為![]() ,當
,當![]() 取得最大值時,求出此時點
取得最大值時,求出此時點![]() 的坐標及
的坐標及![]() 的最大值;
的最大值;
(3)如圖,動點![]() 以每秒
以每秒![]() 個單位長度的速度從點
個單位長度的速度從點![]() 出發,沿射線
出發,沿射線![]() 運動;同時,動點
運動;同時,動點![]() 以每秒
以每秒![]() 個單位長度的速度從點
個單位長度的速度從點![]() 出發,沿射線
出發,沿射線![]() 運動,設運動時間為
運動,設運動時間為![]() (
(![]() ).過
).過![]() 點作
點作![]() 軸,交拋物線于點
軸,交拋物線于點![]() ,當點
,當點![]() 、
、![]() 、
、![]() 所組成的三角形是直角三角形時,直接寫出
所組成的三角形是直角三角形時,直接寫出![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,真命題是( )
A. 相等的角是對頂角
B. 兩條直線被第三條直線所截,同位角相等
C. 在同一平面內,垂直于同一條直線的兩條直線平行
D. 同旁內角互補
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:拋物線y=x2+4x+4+m的圖像與y軸交于點C,點B與點C的縱坐標相同,一次函數y=kx+b的與二次函數交于A、B兩點,且A點坐標為(-1,0).
(1)求二次函數與一次函數的解析式;
(2)若拋物線對稱軸上存在一點P,直線PC將△ABC分成面積為1:2兩部分,求P點坐標。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線C1:![]() 的頂點為P,點Q是x軸正半軸上一點,將拋物線C1繞點Q旋轉180后得到拋物線C2.拋物線C2的頂點為N,與x軸相交于E、F兩點(點E在點F的左邊),當以點P、N、F為頂點的三角形是直角三角形時,則點Q的坐標是______________.
的頂點為P,點Q是x軸正半軸上一點,將拋物線C1繞點Q旋轉180后得到拋物線C2.拋物線C2的頂點為N,與x軸相交于E、F兩點(點E在點F的左邊),當以點P、N、F為頂點的三角形是直角三角形時,則點Q的坐標是______________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com