
【題目】正方形![]() 的邊長為
的邊長為![]() ,點
,點![]() 分別是線段
分別是線段![]() 上的動點,連接
上的動點,連接![]() 并延長,交邊
并延長,交邊![]() 于
于![]() ,過
,過![]() 作
作![]() ,垂足為
,垂足為![]() ,交邊
,交邊![]() 于點
于點![]() .
.
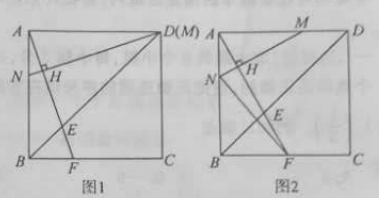
(1)如圖1,若點![]() 與點
與點![]() 重合,求證:
重合,求證:![]() ;
;
(2)如圖2,若點![]() 從點
從點![]() 出發,以
出發,以![]() 的速度沿
的速度沿![]() 向點
向點![]() 運動,同時點
運動,同時點![]() 從點
從點![]() 出發,以
出發,以![]() 的速度沿
的速度沿![]() 向點
向點![]() 運動,運動時間為
運動,運動時間為![]() .
.
①設![]() ,求
,求![]() 關于t的函數表達式;
關于t的函數表達式;
②當![]() 時,連接
時,連接![]() ,求
,求![]() 的長.
的長.
【答案】(1)詳見解析;(2)①![]() ;②5.
;②5.
【解析】
試題分析:(1)根據已知條件易證△ABF≌△NAD,由全等三角形的性質即可得![]() ;(2)
;(2)
先證△ABF∽△NAD,根據全等三角形的性質求得![]() ;(3)利用△ABF∽△NAD,求得t=2,根據(2)的函數解析式求得BF的長,再由勾股定理即可得FN的長.
;(3)利用△ABF∽△NAD,求得t=2,根據(2)的函數解析式求得BF的長,再由勾股定理即可得FN的長.
試題解析:
【解】
(1)∵正方形![]()
∴AD=AB,∠DAN=∠FBA=90°
∵![]()
∴∠NAH+∠ANH=90°
∵∠NDA+∠ANH=90°
∴∠NAH=∠NDA
∴△ABF≌△NAD
∴![]()
(2)①∵正方形![]()
∴AD∥BF
∴∠ADE=∠FBE
∵∠AED=∠BEF
∴△EBF∽△EAD
∴![]()
∵正方形![]()
∴AD=DC=CB=6
∴BD=![]()
∵點![]() 從點
從點![]() 出發,以
出發,以![]() 的速度沿
的速度沿![]() 向點
向點![]() 運動,運動時間為
運動,運動時間為![]() .
.
∴BE=![]() ,DE=
,DE=![]()
∴![]()
∴![]()
②當![]() 時,連接
時,連接![]() ,求
,求![]() 的長.
的長.
∵正方形![]()
∴∠MAN=∠FBA=90°
∵![]()
∴∠NAH+∠ANH=90°
∵∠NMA+∠ANH=90°
∴∠NAH=∠NMA
∴△ABF∽△NAD
∴![]()
∵![]() ,AB=6
,AB=6
∴AN=2,BN=4
∴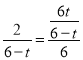
∴t=2
把t=2代入![]() ,得y=3,即BF=3,
,得y=3,即BF=3,
在RT△BFN中,BF=3,BN=4,
根據勾股定理即可得FN=5.


科目:初中數學 來源: 題型:
【題目】(本小題滿分9分)
為了考察甲、乙兩種成熟期小麥的株高長勢狀況,現從中各隨機抽取6株,并測得它們的株高(單位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)請分別計算表內兩組數據的方差,并借此比較哪種小麥的株高長勢比較整齊?
(2)現將進行兩種小麥優良品種雜交試驗,需從表內的甲、乙兩種小麥中,各隨機抽取一株進行配對,以預估整體配對狀況.請你用列表法或畫樹狀圖的方法,求所抽取的兩株配對小麥株高恰好都等于各自平均株高的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校有21名同學們參加某比賽,預賽成績各不同,要取前11名參加決賽,小穎已經知道了自己的成績,她想知道自己能否進入決賽,只需要再知道這21名同學成績的( )
A.最高分
B.中位數
C.極差
D.平均數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把矩形ABCD沿EF翻折,點B恰好落在AD邊的B′處,若AE=2,DE=6,∠EFB=60°,則矩形ABCD的面積是( ) 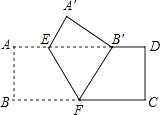
A.12
B.24
C.12 ![]()
D.16 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
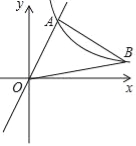
【題目】如圖,在平面直角坐標系中,經過點A的雙曲線y=![]() (x>0)同時經過點B,且點A在點B的左側,點A的橫坐標為
(x>0)同時經過點B,且點A在點B的左側,點A的橫坐標為![]() ,∠AOB=∠OBA=45°,則k的值為 .
,∠AOB=∠OBA=45°,則k的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數![]() (a是常數,a≠0),下列結論正確的是( )
(a是常數,a≠0),下列結論正確的是( )
A.當a=1時,函數圖象經過點(﹣1,1)
B.當a=﹣2時,函數圖象與x軸沒有交點
C.若a<0,函數圖象的頂點始終在x軸的下方
D.若a>0,則當x≥1時,y隨x的增大而增大
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com