
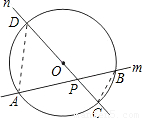
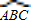 的中點,弦DE⊥AB于點F.請找出點C和點E重合的條件,并說明理由.
的中點,弦DE⊥AB于點F.請找出點C和點E重合的條件,并說明理由.
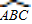 的中點,根據2∠CAD=∠CAD+ACD=180°-∠ABC,就可以求出∠BAC的度數.
的中點,根據2∠CAD=∠CAD+ACD=180°-∠ABC,就可以求出∠BAC的度數.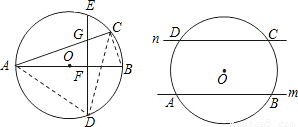
 的中點,所以2∠CAD=∠CAD+∠ACD=180°-∠ABC,
的中點,所以2∠CAD=∠CAD+∠ACD=180°-∠ABC, 或AF=3•FB等也可,評分可參照上面的標準;也可以先直覺猜測點B、C是圓的十二等分點,然后說明.)
或AF=3•FB等也可,評分可參照上面的標準;也可以先直覺猜測點B、C是圓的十二等分點,然后說明.)

科目:初中數學 來源: 題型:
 | ABC |
 ⊥AB于點F.請找出點C和點E重合的條件,并說明理由.
⊥AB于點F.請找出點C和點E重合的條件,并說明理由.查看答案和解析>>
科目:初中數學 來源:第28章《圓》中考題集(22):28.1 圓的認識(解析版) 題型:解答題
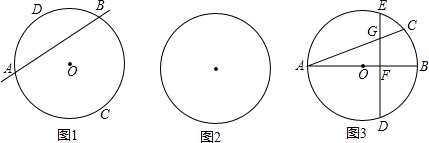
 的中點,弦DE⊥AB于點F.請找出點C和點E重合的條件,并說明理由.
的中點,弦DE⊥AB于點F.請找出點C和點E重合的條件,并說明理由.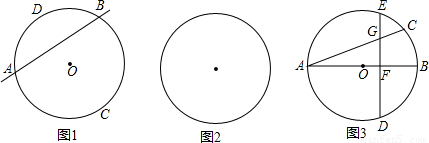
查看答案和解析>>
科目:初中數學 來源:第5章《中心對稱圖形(二)》中考題集(21):5.3 圓周角(解析版) 題型:解答題
 的中點,弦DE⊥AB于點F.請找出點C和點E重合的條件,并說明理由.
的中點,弦DE⊥AB于點F.請找出點C和點E重合的條件,并說明理由.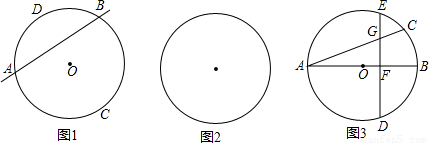
查看答案和解析>>
科目:初中數學 來源:2008年全國中考數學試題匯編《圓》(11)(解析版) 題型:解答題
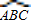 的中點,弦DE⊥AB于點F.請找出點C和點E重合的條件,并說明理由.
的中點,弦DE⊥AB于點F.請找出點C和點E重合的條件,并說明理由.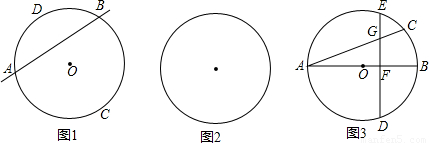
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com