【題目】在平面直角坐標系中，點A（1，1），B（4，3），將點A向左平移2個單位長度，再向上平移3個單位長度得到點C．
（1）寫出點C的坐標；
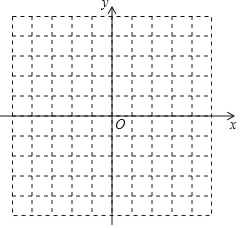
（2）畫出△ABC并判斷△ABC的形狀．
【答案】（1）C（﹣1，4）；（2）△ABC是等腰直角三角形；過程見詳解.
【解析】
（1）根據向左平移2個單位長度為橫坐標減2，向上平移3個單位長度為縱坐標加3，即可得到C點坐標.
（2）如圖，順次連接A，B，C，然后根據每個點的坐標利用兩點間的距離公式分別求出AB，BC，CA的長，再根據勾股定理逆定理判斷即可.
（1）∵將點A（1，1）向左平移2個單位長度，再向上平移3個單位長度得到點C，
∴C（﹣1，4）；
（2）△ABC是等腰直角三角形；
如圖所示，根據勾股定理得，AB=
=
=
，
BC=
=
=
，
AC=
=
=，
∴AB=AC，
∵AB2+AC2=BC2=26，
∴△ABC是直角三角形，
∴△ABC是等腰直角三角形．
科目：初中數學 來源： 題型：
【題目】如圖，某容器由A、B、C三個連通長方體組成，其中A、B、C的底面積分別為25cm2、10cm2、5cm2，C的容積是整個容器容積的
（容器各面的厚度忽略不計），A、B的總高度為12厘米．現以均勻的速度（單位：cm3/min）向容器內注水，直到注滿為止．已知單獨注滿A、B分別需要的時間為10分鐘、8分鐘．
（1）求注滿整個容器所需的總時間；
（2）設容器A的高度為xcm，則容器B的高度為 cm；
（3）求容器A的高度和注水的速度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，某地有一地下工程，其底面是正方形，面積為405m2，四個角是面積為5m2的小正方形滲水坑，根據這些條件如何求a的值？與你的同伴進行交流．
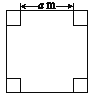
下面是小康提供的解題方案，根據解題方案請你完成本題的解答過程：
①設大正方形的邊長為x m，小正方形的邊長為y m，那么根據題意可列出關于x的方程為_______，關于y的方程為_______；
②利用平方根的意義，可求得x＝________(取正值，結果保留根號)，y＝________(取正值，結果保留根號)；
③所以a＝x－2y＝____________＝__________(結果保留根號)；
④答：________________________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，拋物線y=ax2+bx+c與x軸相交于點B（1，0）和點C（9，0）兩點，與y軸的負半軸相交于A點，過A、B、C三點的⊙P與y軸相切于點A，M為y軸正半軸上的一個動點，直線MB交⊙P于點D，交拋物線于點N．
（1）求點A坐標和⊙P的半徑；
（2）求拋物線的解析式；
（3）當△MOB與以點B、C、D為頂點的三角形相似時，求△CDN的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了進一步普及足球知識，傳播足球文化，某市舉行了“足球進校園”知識競賽活動，為了解足球知識的普及情況，隨機抽取了部分獲獎情況進行整理，得到下列不完整的統計圖表：
獲獎等次 | 頻數 | 頻率 |
一等獎 | 10 | 0.05 |
二等獎 | 20 | 0.10 |
三等獎 | 30 | b |
優勝獎 | a | 0.30 |
鼓勵獎 | 80 | 0.40 |
請根據所給信息，解答下列問題：
（1）a= ， b=；
（2）補全頻數分布直方圖；
（3）在這次競賽中，甲、乙、丙、丁四位同學都獲得一等獎，若從這四位同學中隨機選取兩位同學代表該市參加上一級競賽，請用樹狀圖或列表的方法，計算恰好選中甲、乙二人的概率． 
查看答案和解析>>
科目：初中數學 來源： 題型：
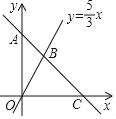
【題目】一次函數y=kx+b的圖象經過點A（0，9），并且與直線y=
x相交于點B，與x軸相交于點C．
（1）若點B的橫坐標為3，求B點的坐標和k，b的值；
（2）在y軸上是否存在這樣的點P，使得以點P，B，A為頂點的三角形是等腰三角形？若存在，請直接寫出點P坐標；若不存在，請說明理由．
（3）在直線y=kx+b上是否存在點Q，使△OBQ的面積等于
？若存在，請求出點Q的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在折紙活動中，小明制作了一張△ABC紙片，點D、E分別是邊AB、AC上，將△ABC沿著DE折疊壓平，A與A′重合，若∠A=75°，則∠1+∠2=（ ） 
A.150°
B.210°
C.105°
D.75°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）一個兩位正整數，a表示十位上的數字，b表示個位上的數字（a≠b，ab≠0），則這個兩位數用多項式表示為 （含a、b的式子）；若把十位、個位上的數字互換位置得到一個新兩位數，則這兩個兩位數的和一定能被 整除，這兩個兩位數的差一定能被 整除
（2）一個三位正整數F，各個數位上的數字互不相同且都不為0．若從它的百位、十位、個位上的數字中任意選擇兩個數字組成6個不同的兩位數．若這6個兩位數的和等于這個三位數本身，則稱這樣的三位數F為“友好數”，例如：132是“友好數”
一個三位正整數P，各個數位上的數字互不相同且都不為0，若它的十位數字等于百位數字與個位數字的和，則稱這樣的三位數P為“和平數”
①直接判斷123是不是“友好數”？
②直接寫出共有 個“和平數”
③通過列方程的方法求出既是“和平數”又是“友好數”的數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
