
【題目】下列哪一個是假命題( )
A.五邊形外角和為 ![]()
B.切線垂直于經過切點的半徑
C.![]() 關于
關于 ![]() 軸的對稱點為
軸的對稱點為 ![]()
![]()
D.拋物線 ![]() 對稱軸為直線
對稱軸為直線 ![]()
【答案】C
【解析】解:A.多邊形的外角和為360°,故本選項正確.
B.切線垂直于過切點的半徑,故本選項正確.
C.(3,-2)關于y的對稱點為(-3,-2),故本選項錯誤.
D.拋物線y=x2-4x+2017對稱軸為直線x=2.故本選項正確.
所以答案是C.
【考點精析】利用二次函數的性質和多邊形內角與外角對題目進行判斷即可得到答案,需要熟知增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小;多邊形的內角和定理:n邊形的內角和等于(n-2)180°.多邊形的外角和定理:任意多邊形的外角和等于360°.


科目:初中數學 來源: 題型:
【題目】為發展校園足球運動,某縣城區四校決定聯合購買一批足球運動裝備,市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球,已知每套隊服比每個足球多50元,兩套隊服與三個足球的費用相等,經洽談,甲商場優惠方案是:每購買十套隊服,送一個足球;乙商場優惠方案是:若購買隊服超過80套,則購買足球打八折.
(1)求每套隊服和每個足球的價格是多少?
(2)若城區四校聯合購買100套隊服和a個足球,請用含a的式子分別表示出到甲商場和乙商場購買裝備所花的費用;
(3)假如你是本次購買任務的負責人,你認為到哪家商場購買比較合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
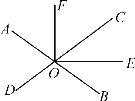
【題目】如圖,直線AB,CD相交于點O,OE是∠COB的平分線,∠FOE=90°,若∠AOD=70°.
(1)求∠BOE的度數;
(2)OF是∠AOC的平分線嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
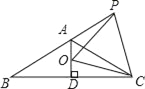
【題目】如圖,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于點D,點P是BA延長線上一點,點O是線段AD上一點,OP=OC.
(1)求∠APO+∠DCO的度數;
(2)求證:點P在OC的垂直平分線上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級(1)班的全體同學根據自己的興趣愛好參加了六個學生社團(每個學生必須參加且只參加一個),為了了解學生參加社團的情況,學生會對該班參加各個社團的人數進行了統計,繪制成了如圖不完整的扇形統計圖,已知參加“讀書社”的學生有10人,請解答下列問題: 
(1)該班的學生共有名;該班參加“愛心社”的人數為名,若該班參加“吉他社”與“街舞社”的人數相同,則“吉他社”對應扇形的圓心角的度數為;
(2)一班學生甲、乙、丙是“愛心社”的優秀社員,現要從這三名學生中隨機選兩名學生參加“社區義工”活動,請你用畫樹狀圖或列表的方法求出恰好選中甲和乙的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC經過一次平移到△DFE的位置,請回答下列問題:
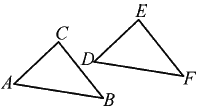
(1)點C的對應點是點__________,∠D=__________,BC=__________;
(2)連接CE,那么平移的方向就是__________的方向,平移的距離就是線段__________的長度;
(3)連接AD,BF,BE,與線段CE相等的線段有__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】深圳市某學校抽樣調查,A類學生騎共享單車,B類學生坐公交車、私家車等,C類學生步行,D類學生(其它),根據調查結果繪制了不完整的統計圖.
類型 | 頻數 | 頻率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
(1)學生共人, ![]() ,
, ![]() ;
;
(2)補全條形統計圖;
(3)若該校共有2000人,騎共享單車的有人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】概念學習
規定:如果一個三角形的三個角分別等于另一個三角形的三個角,那么稱這兩個三角形互為“等角三角形”.
從三角形![]() 不是等腰三角形
不是等腰三角形![]() 一個頂點引出一條射線與對邊相交,頂點與交點之間的線段把這個三角形分割成兩個小三角形,如果分得的兩個小三角形中一個為等腰三角形,另一個與原來三角形是“等角三角形”,我們把這條線段叫做這個三角形的“等角分割線”.
一個頂點引出一條射線與對邊相交,頂點與交點之間的線段把這個三角形分割成兩個小三角形,如果分得的兩個小三角形中一個為等腰三角形,另一個與原來三角形是“等角三角形”,我們把這條線段叫做這個三角形的“等角分割線”.
理解概念
![]() 如圖1,在
如圖1,在![]() 中,
中,![]() ,
,![]() ,請寫出圖中兩對“等角三角形”
,請寫出圖中兩對“等角三角形”![]() 概念應用
概念應用
![]() 如圖2,在
如圖2,在![]() 中,CD為角平分線,
中,CD為角平分線,![]() ,
,![]() .
.
求證:CD為![]() 的等角分割線.
的等角分割線.
![]() 在
在![]() 中,
中,![]() ,CD是
,CD是![]() 的等角分割線,直接寫出
的等角分割線,直接寫出![]() 的度數.
的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
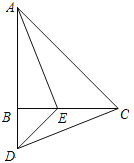
【題目】如圖,在△ABC中,AB=CB,∠ABC=90°,D為AB延長線上一點,點E在BC邊上,且BE=BD,連結AE、DE、DC.
① 求證:△ABE≌△CBD;
② 若∠CAE=30°,求∠BDC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com