
【題目】通過類比聯想、引申拓展研究典型題目,可達到解一題知一類的目的.下面是一個案例,請補充完整.
原題:如圖1,點E、F分別在正方形ABCD的邊BC、CD上,∠EAF=45°,
連接EF,則EF=BE+DF,試說明理由.

(1)思路梳理
∵AB=AD
∴把△ABE繞點A逆時針旋轉90°至△ADG,可使AB與AD重合
∵∠ADC=∠B=90°
∴∠FDG=180°
∴點F、D、G共線
根據 ,易證△AFG≌ ,進而得EF=BE+DF.
(2)聯想拓展
如圖2,在△ABC中,∠BAC=90°,AB=AC,點D、E均在邊BC上,且∠DAE=45°.猜想BD、DE、EC應滿足的數量關系,并寫出推理過程.
【答案】(1)SAS;△AFE;(2) BD2+EC2=DE2
【解析】
試題分析:(1)根據三角形全等的條件可求解;
(2)根據旋轉的性質和全等三角形的性質與判定可求解.
試題解析:(1)SAS;△AFE
(2)把△ABD繞A點逆時針旋轉90°至△ACG,可使AB與AC重合,根據旋轉的性質,全等三角形的性質和勾股定理,可得到BD2+EC2=DE2。
推理過程如下:
∵AB=AC,
∴把△ABD繞A點逆時針旋轉90°至△ACG,可使AB與AC重合(如圖)。

且△ACG≌△ABD
∴AG=AD
∵△ABC中,∠BAC=90°,
∴∠ACB+∠ACG=∠ACB+∠B=90°,即∠ECG=90°。
∴EC2+CG2=EG2。
在△AEG與△AED中,
∠EAG=∠EAD。
AD=AG,AE=AE,
∴△AEG≌△AED(SAS)。
∴DE=EG。
又∵CG=BD,
∴BD2+EC2=DE2


科目:初中數學 來源: 題型:
【題目】在某市組織的大型商業演出活動中,對團體購買門票實行優惠,決定在原定票價基礎上每張降價80元,這樣按原定票價需花費6000元購買的門票張數,現在只花費了4800元.
(1)求每張門票的原定票價;
(2)根據實際情況,活動組織單位決定對于個人購票也采取優惠政策,原定票價經過連續二次降價后降為324元,求平均每次降價的百分率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小龍在學校組織的社會調查活動中負責了解他所居住的小區450戶居民的家庭收入情況、他從中隨機調查了40戶居民家庭收入情況(收入取整數,單位:元),并繪制了如下的頻數分布表和頻數分布直方圖:
分組 | 頻數 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合計 | 40 | 100% |
根據以上提供的信息,解答下列問題:
(1)補全頻數分布表;
(2)補全頻數分布直方圖;

(3)請你估計該居民小區家庭屬于中等收入(大于1000不足1600元)的大約有多少戶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC的三個頂點的坐標分別為A(﹣2,3)、B(﹣6,0)、C(﹣1,0). 
(1)請直接寫出點A關于y軸對稱的點的坐標;
(2)將△ABC繞坐標原點O逆時針旋轉90度.畫出圖形,直接寫出點B的對應點的坐標;
(3)請直接寫出:以A、B、C為頂點的平行四邊形的第四個頂點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c的圖象如圖所示,則一元二次方程ax2+bx+c=0( ) 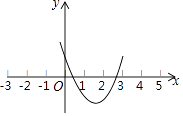
A.沒有實根
B.只有一個實根
C.有兩個實根,且一根為正,一根為負
D.有兩個實根,且一根小于1,一根大于2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學校開展的綜合實踐活動中,某班進行了小制作評比,作品上交時間為5月1日到30日,評委會把同學們上交作品的件數按5天一組分組統計,繪制了頻數分布直方圖(如圖所示).已知從左至右各長方形的高的比為2∶3∶4∶6∶4∶1,第三組的頻數為12,請解答下列問題:
(1)本次活動共有多少件作品參加評比?
(2)哪組上交的作品數量最多?有多少件?
(3)哪組上交的作品數量最少?有多少件?
(4)第二組上交的作品數量是多少件?
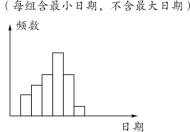
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】相傳有個人不講究說話藝術常引起誤會,一天他擺宴席請客,他看到還有幾個人沒來,就自言自語:“怎么該來的還不來啊?”客人聽了心里想難道我們是不該來的,于是有一半客人走了.他一看十分著急,又說:“不該走的倒走了!”剩下的人一聽,是我們該走啊!又有剩下的三分之二的人離開了.他著急地一拍大腿,連說:“我說的不是他們.”于是最后剩下的四個人也都告辭走了.聰明的你能知道剛開始來的客人個數是( )
A. 24 B. 18 C. 16 D. 15
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知菱形ABCD中,AB=6,∠B=60°.E是BC邊上一動點,F是CD邊上一動點,且BE=CF,連接AE、AF.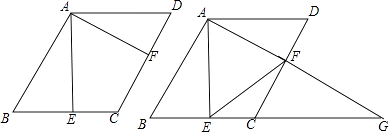
(1)∠EAF的度數是;
(2)求證:AE=AF;
(3)延長AF交BC的延長線于點G,連接EF,設BE=x,EF2=y,求y與x之間的函數關系式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com