
【題目】已知二次函數y=ax2﹣2ax+c(a<0)的最大值為4,且拋物線過點( ![]() ,﹣
,﹣ ![]() ),點P(t,0)是x軸上的動點,拋物線與y軸交點為C,頂點為D.
),點P(t,0)是x軸上的動點,拋物線與y軸交點為C,頂點為D.
(1)求該二次函數的解析式,及頂點D的坐標;
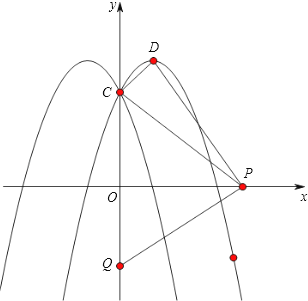
(2)求|PC﹣PD|的最大值及對應的點P的坐標;
(3)設Q(0,2t)是y軸上的動點,若線段PQ與函數y=a|x|2﹣2a|x|+c的圖象只有一個公共點,求t的取值.
【答案】
(1)
解:∵y=ax2﹣2ax+c的對稱軸為:x=﹣ ![]() =1,
=1,
∴拋物線過(1,4)和( ![]() ,﹣
,﹣ ![]() )兩點,
)兩點,
代入解析式得: 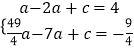 ,
,
解得:a=﹣1,c=3,
∴二次函數的解析式為:y=﹣x2+2x+3,
∴頂點D的坐標為(1,4);
(2)
解:∵C、D兩點的坐標為(0,3)、(1,4);
由三角形兩邊之差小于第三邊可知:
|PC﹣PD|≤|CD|,
∴P、C、D三點共線時|PC﹣PD|取得最大值,此時最大值為,
|CD|= ![]() ,
,
由于CD所在的直線解析式為y=x+3,
將P(t,0)代入得t=﹣3,
∴此時對應的點P為(﹣3,0)
(3)
解:y=a|x|2﹣2a|x|+c的解析式可化為:
y= ![]()
設線段PQ所在的直線解析式為y=kx+b,將P(t,0),Q(0,2t)代入得:
線段PQ所在的直線解析式:y=﹣2x+2t,
∴①當線段PQ過點(0,3),即點Q與點C重合時,線段PQ與函數
y= ![]() 有一個公共點,此時t=
有一個公共點,此時t= ![]() ,
,
當線段PQ過點(3,0),即點P與點(3,0)重合時,t=3,此時線段PQ與
y= ![]() 有兩個公共點,所以當
有兩個公共點,所以當 ![]() ≤t<3時,
≤t<3時,
線段PQ與y= ![]() 有一個公共點,
有一個公共點,
②將y=﹣2x+2t代入y=﹣x2+2x+3(x≥0)得:
﹣x2+2x+3=﹣2x+2t,
﹣x2+4x+3﹣2t=0,
令△=16﹣4(﹣1)(3﹣2t)=0,
t= ![]() >0,
>0,
所以當t= ![]() 時,線段PQ與y=
時,線段PQ與y= ![]() 也有一個公共點,
也有一個公共點,
③當線段PQ過點(﹣3,0),即點P與點(﹣3,0)重合時,線段PQ只與
y=﹣x2﹣2x+3(x<0)有一個公共點,此時t=﹣3,
所以當t≤﹣3時,線段PQ與y= ![]() 也有一個公共點,
也有一個公共點,
綜上所述,t的取值是 ![]() ≤t<3或t=
≤t<3或t= ![]() 或t≤﹣3.
或t≤﹣3.
【解析】(1)先利用對稱軸公式x=﹣ ![]() 計算對稱軸,即頂點坐標為(1,4),再將兩點代入列二元一次方程組求出解析式;
計算對稱軸,即頂點坐標為(1,4),再將兩點代入列二元一次方程組求出解析式;
(2)根據三角形的三邊關系:可知P、C、D三點共線時|PC﹣PD|取得最大值,求出直線CD與x軸的交點坐標,就是此時點P的坐標;
(3)先把函數中的絕對值化去,可知y= 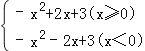 ,此函數是兩個二次函數的一部分,分三種情況進行計算:①當線段PQ過點(0,3),即點Q與點C重合時,兩圖象有一個公共點,當線段PQ過點(3,0),即點P與點(3,0)重合時,兩函數有兩個公共點,寫出t的取值;②線段PQ與當函數y=a|x|2﹣2a|x|+c(x≥0)時有一個公共點時,求t的值;③當線段PQ過點(﹣3,0),即點P與點(﹣3,0)重合時,線段PQ與當函數y=a|x|2﹣2a|x|+c(x<0)時也有一個公共點,則當t≤﹣3時,都滿足條件;綜合以上結論,得出t的取值.本題考查了二次函數的綜合應用,先利用待定系數法求解析式,同時把最大值與三角形的三邊關系聯系在一起;同時對于二次函數利用動點求取值問題,從特殊點入手,把函數分成幾部分考慮,按自變量從大到小的順序或從小到大的順序求解.
,此函數是兩個二次函數的一部分,分三種情況進行計算:①當線段PQ過點(0,3),即點Q與點C重合時,兩圖象有一個公共點,當線段PQ過點(3,0),即點P與點(3,0)重合時,兩函數有兩個公共點,寫出t的取值;②線段PQ與當函數y=a|x|2﹣2a|x|+c(x≥0)時有一個公共點時,求t的值;③當線段PQ過點(﹣3,0),即點P與點(﹣3,0)重合時,線段PQ與當函數y=a|x|2﹣2a|x|+c(x<0)時也有一個公共點,則當t≤﹣3時,都滿足條件;綜合以上結論,得出t的取值.本題考查了二次函數的綜合應用,先利用待定系數法求解析式,同時把最大值與三角形的三邊關系聯系在一起;同時對于二次函數利用動點求取值問題,從特殊點入手,把函數分成幾部分考慮,按自變量從大到小的順序或從小到大的順序求解.


科目:初中數學 來源: 題型:
【題目】為了豐富學生課外小組活動,培養學生動手操作能力,王老師讓學生把5m長的彩繩截成2m或1m的彩繩,用來做手工編織,在不造成浪費的前提下,你有幾種不同的截法( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為調查本校學生周末平均每天做作業所用時間的情況,隨機調查了50名同學,下圖是根據調查所得數據繪制的統計圖的一部分.

請根據以上信息,解答下列問題:
(1)在這次調查的數據中,做作業所用時間的眾數是 ,中位數是 ,平均數是 ;
(2)若該校共有2000名學生,根據以上調查結果估計該校全體學生每天做作業時間在3小時內(含3小時)的同學共有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分別是AB、AD、CB上的點,AM=CE=1,AN=3,點P從點M出發,以每秒1個單位長度的速度沿折線MB﹣BE向點E運動,同時點Q從點N出發,以相同的速度沿折線ND﹣DC﹣CE向點E運動,當其中一個點到達后,另一個點也停止運動.設△APQ的面積為S,運動時間為t秒,則S與t函數關系的大致圖象為( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=ax2﹣6x+c與x軸交于點A(﹣5,0)、B(﹣1,0),與y軸交于點C(0,﹣5),點P是拋物線上的動點,連接PA、PC,PC與x軸交于點D.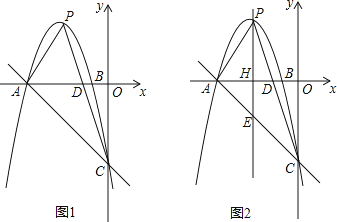
(1)求該拋物線所對應的函數解析式;
(2)若點P的坐標為(﹣2,3),請求出此時△APC的面積;
(3)過點P作y軸的平行線交x軸于點H,交直線AC于點E,如圖2.
①若∠APE=∠CPE,求證: ![]() ;
;
②△APE能否為等腰三角形?若能,請求出此時點P的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
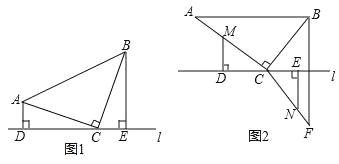
【題目】直角三角形ABC中,∠ACB=90°,直線l過點 C.
(1)當AC=BC時,如圖1,分別過點A和B作AD⊥直線l于點D,BE⊥直線l于點 E.△ACD與△CBE是否全等,并說明理由;
(2)當AC=8cm,BC=6cm時,如圖2,點B與點F關于直線l對稱,連接BF、CF.點M是AC上一點,點N是CF上一點,分別過點M、N作MD⊥直線l于點D,NE⊥直線l于點E,點M從A點出發,以每秒1cm的速度沿A→C路徑運動,終點為 C.點N從點F出發,以每秒3cm的速度沿F→C→B→C→F路徑運動,終點為F.點M、N同時開始運動,各自達到相應的終點時停止運動,設運動時間為t秒.
①當△CMN為等腰直角三角形時,求t的值;
②當△MDC與△CEN全等時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知A(a,0),B (0,b)分別為兩坐標軸上的點,且a,b滿足a2﹣24a+|b﹣12|=﹣144,且3OC=OA.
(1)求A、B、C三點的坐標;
(2)若D(2,0),過點D的直線分別交AB、BC于E、F兩點,且DF=DE,設E、F兩點的橫坐標分別為xE、xP,求xE+xP的值;
(3)如圖2,若M(4,8),點P是x軸上A點右側一動點,AH⊥PM于點H,在HM上取點G,使HG=HA,連接CG,當點P在點A右側運動時,∠CGM的度數是否改變?若不變,請求其值;若改變,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】深圳市政府計劃投資1.4萬億元實施東進戰略.為了解深圳市民對東進戰略的關注情況.某校數學興趣小組隨機采訪部分深圳市民,對采訪情況制作了統計圖表的一部分如下:
關注情況 | 頻數 | 頻率 |
A.高度關注 | M | 0.1 |
B.一般關注 | 100 | 0.5 |
C.不關注 | 30 | N |
D.不知道 | 50 | 0.25 |

(1)根據上述統計圖可得此次采訪的人數為人,m= , n=
(2)根據以上信息補全條形統計圖;
(3)根據上述采訪結果,請估計在15000名深圳市民中,高度關注東進戰略的深圳市民約有人.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com