Question

在數學課上，老師給出以下條件和問題，要求同學們探索并得出結論：
（1）點A₁，A₂，A₃是拋物線y=2x²圖象上的三點，若A₁，A₂，A₃三點的橫坐標從左至右依次為1，2，3，求△A₁A₂A₃的面積；
（2）若將（1）中的拋物線改為y=2x²-4x+7，其他條件不變，那么△A₁A₂A₃的面積變不變？請求出△A₁A₂A₃的面積；
（3）若將拋物線改為y=ax²+bx+c （a＞0），其他條件不變，那么△A₁A₂A₃的面積又是多少呢？請說明理由；
（4）從中你發現了什么規律？請用一句話簡單歸納．

Answer 1

解：（1）當點A₁ A₂ A₃是拋物線y=2x²圖象上的三點，
若A₁，A₂，A₃，三點的橫坐標從左至右依次為1，2，3，
∴A₁，A₂，A₃三點的縱坐標從左至右依次為2，8，18，
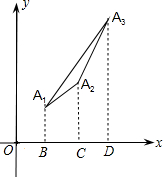
∴S_△A1A2A3=S_梯形A1BDA3-S_梯形A1BCA2-S_梯形A2CDA3=×（2+18）×2-×（8+18）×1-×（2+8）×1=2；

（2）若將（1）中的拋物線改為y=2x²-4x+7，
其他條件不變，那么△A₁A₂A₃的面積不變，即：△A₁A₂A₃的面積為2；

（3）若將拋物線改為y=ax²+bx+c （a＞0），
∵若A₁，A₂，A₃，三點的橫坐標從左至右依次為1，2，3，
∴A₁，A₂，A₃三點的縱坐標從左至右依次為a+b+c，4a+2b+c，9a+3b+c，
∴S_△A1A2A3=S_梯形A1BDA3-S_梯形A1BCA2-S_梯形A2CDA3=×（a+b+c+9a+3b+c）×2-×（a+b+c+4a+2b+c）×1-×（4a+2b+c+9a+3b+c）×1=a；
∴△A₁A₂A₃的面積為a；

（4）從中發現規律：若點A₁ A₂ A₃是拋物線y=ax²+bx+c圖象上的三點，
且A₁，A₂，A₃，三點的橫坐標從左至右依次為1，2，3，
則△A₁A₂A₃的面積等于二次項系數的絕對值．----
分析：（1）由點A₁，A₂，A₃是拋物線y=2x²圖象上的三點，若A₁，A₂，A₃三點的橫坐標從左至右依次為1，2，3，即可求得A₁，A₂，A₃三點的縱坐標，又由S_△A1A2A3=S_梯形A1BDA3-S_梯形A1BCA2-S_梯形A2CDA3，即可求得△A₁A₂A₃的面積；
（2）解法同（1），即可得其他條件不變，那么△A₁A₂A₃的面積不變，即△A₁A₂A₃的面積為2；
（3）由點A₁，A₂，A₃是拋物線y=ax²+bx+c （a＞0）圖象上的三點，若A₁，A₂，A₃三點的橫坐標從左至右依次為1，2，3，即可求得A₁，A₂，A₃三點的縱坐標，又由S_△A1A2A3=S_梯形A1BDA3-S_梯形A1BCA2-S_梯形A2CDA3，即可求得△A₁A₂A₃的面積；
（4）可得規律：若點A₁ A₂ A₃是拋物線y=ax²+bx+c圖象上的三點，且A₁，A₂，A₃，三點的橫坐標從左至右依次為1，2，3，則△A₁A₂A₃的面積等于二次項系數的絕對值
點評：此題考查了點與二次函數的關系以及三角形面積的求解方法．此題難度較大，解題的關鍵是抓住△A₁A₂A₃的面積的求解方法，注意S_△A1A2A3=S_梯形A1BDA3-S_梯形A1BCA2-S_梯形A2CDA3，注意數形結合思想的應用．