
【題目】閱讀下列材料并完成任務:
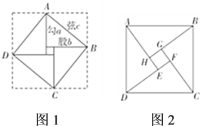
中國古代三國時期吳國的數學家趙爽最早對勾股定理作出理論證明.他創制了一幅“勾股圓方圖”(如圖l),用數形結合的方法,給出了勾股定理的詳細證明.在這幅“勾股圓方圖”中,以弦為邊長得到的正方形![]() 是由
是由![]() 個全等的直角三角形再加上中間的那個小正方形組成的.每個直角三角形的面積為
個全等的直角三角形再加上中間的那個小正方形組成的.每個直角三角形的面積為![]() ;中間的小正方形邊長為
;中間的小正方形邊長為![]() ,面積為
,面積為![]() .于是便得到式子:
.于是便得到式子:![]() .趙爽的這個證明可謂別具匠心,極富創新意識.他用幾何圖形的截、割、拼、補來證明代數式之間的恒等關系,既具嚴密性,又具直觀性,為中國古代以形證數、形數統一、代數和幾何緊密結合、互不可分的獨特風格樹立了一個典范.如圖2,是“趙爽弦圖”,其中
.趙爽的這個證明可謂別具匠心,極富創新意識.他用幾何圖形的截、割、拼、補來證明代數式之間的恒等關系,既具嚴密性,又具直觀性,為中國古代以形證數、形數統一、代數和幾何緊密結合、互不可分的獨特風格樹立了一個典范.如圖2,是“趙爽弦圖”,其中![]() 、
、![]() 、
、![]() 和
和![]() 是四個全等的直角三角形,四邊形
是四個全等的直角三角形,四邊形![]() 和
和![]() 都是正方形,根據這個圖形的面積關系,可以證明勾股定理.設
都是正方形,根據這個圖形的面積關系,可以證明勾股定理.設![]() ,
,![]() ,
,![]() ,取
,取![]() ,
,![]() .
.
任務:
(1)填空:正方形![]() 的面積為______,四個直角三角形的面積和為______;
的面積為______,四個直角三角形的面積和為______;
(2)求![]() 的值.
的值.
【答案】(1)4,96;(2)196.
【解析】
(1)根據題意得圖中的四個直角三角形都全等,可得正方形![]() 的邊長為2,即可得正方形
的邊長為2,即可得正方形![]() 的面積;再利用正方形ABCD的面積-正方形EFGH的面積即可得四個直角三角形的面積和;
的面積;再利用正方形ABCD的面積-正方形EFGH的面積即可得四個直角三角形的面積和;
(2)易求得ab的值,和a2+b2的值,根據完全平方公式即可求得(a+b)2的值,即可解題.
(1)根據題意得,圖中的四個直角三角形都全等,
∴AB=c=10,AE-AH=b-a=2,
∴正方形![]() 的面積為22=4,正方形ABCD的面積為102=100,
的面積為22=4,正方形ABCD的面積為102=100,
∴四個直角三角形的面積和=正方形ABCD的面積-正方形EFGH的面積=100-4=96;
(2)由(1)可知四個直角三角形的面積和為![]() ,
,
![]() ,即
,即![]() .
.
![]() ,
,
![]() .
.


科目:初中數學 來源: 題型:
【題目】某歡樂谷為回饋廣大谷迷,在暑假期間推出學生個人門票優惠價,各票價如下:
票價種類 | (A)學生夜場票 | (B)學生日通票 | (C)節假日通票 |
單價(元) | 80 | 120 | 150 |
某慈善單位欲購買三種類型的票共100張獎勵品學兼優的留守學生,其中購買的B種票數是A種票數的3倍還多7張,C種票y張.
(1)直接寫出y與x之間的函數關系式;
(2)設購票總費用為w元,求w(元)與x(張)之間的函數關系式;
(3)為方便學生游玩,計劃購買的學生夜場票不低于20張,且每種票至少購買5張,則有幾種購票方案?并指出哪種方案費用最少.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有下列說法:①如果一個數的立方根等于它本身,那么它一定是1戓0:②無限小數都是無理數;③實數與數軸上的點一一對應;④![]() 是分數;③近似數5.60所表示的準確數的范圍是:5.55≤x<5.65.其中正確的個數是( )
是分數;③近似數5.60所表示的準確數的范圍是:5.55≤x<5.65.其中正確的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】海水養殖是萊州經濟產業的亮麗名片之一,某養殖場響應山東省加快新舊動能轉換的號召,今年采用新技術投資養殖了200萬籠扇貝,并且全部被訂購,已知每籠扇貝的成本是40元,售價是100元,打撈出售過程中發現,一部分扇貝生長情況不合要求,最后只能按照25元一籠出售,如果純收入為![]() 萬元,不合要求的扇貝有
萬元,不合要求的扇貝有![]() 萬籠.
萬籠.
(1)求純收入![]() 關于
關于![]() 的關系式.
的關系式.
(2)當![]() 為何值時,養殖場不賠不嫌?
為何值時,養殖場不賠不嫌?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按要求填空:
(1)填表:
a | 0.0004 | 0.04 | 4 | 400 |
|
(2)根據你發現規律填空:
已知: ![]() =2.638,則
=2.638,則![]() =__,
=__, ![]() =__;
=__;
已知: ![]() =0.06164,
=0.06164, ![]() =61.64,則x=__.
=61.64,則x=__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先化簡,再求值:
閱讀材料,大數學家高斯在上學讀書時曾經研究過這樣一個問題:1+2+3+…+100=?經過研究,這個問題的一般性結論是1+2+3+…+![]() ,其中n是正整數。現在我們來研究一個類似的問題:1×2+2×3+…
,其中n是正整數。現在我們來研究一個類似的問題:1×2+2×3+…![]() =?
=?
觀察下面三個特殊的等式
![]()
![]()
![]()
將這三個等式的兩邊相加,可以得到1×2+2×3+3×4=![]()
讀完這段材料,請你思考后回答:(只需寫出結果,不必寫中間的過程)
(1)![]()
(2)1×2+2×3+3×4+…+n×(n+1)=
(3)![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下面的有理數填在相應的大括號里:15,![]() ,0,12%,-30,0.15,-2.6,-128,
,0,12%,-30,0.15,-2.6,-128,![]() ,-6.4777……,中,
,-6.4777……,中,
整數有:{ };
分數有:{ };
負有理數:{ };
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,△ACD沿AD折疊,使得點C落在斜邊AB上的點E處.

(1)求證:△BDE∽△BAC;
(2)已知AC=6,BC=8,求線段AD的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,把一塊含
,把一塊含![]() 角的三角板
角的三角板![]() 的直角頂點
的直角頂點![]() 放在
放在![]() 的中點上(直角三角板的短直角邊為
的中點上(直角三角板的短直角邊為![]() ,長直角邊為
,長直角邊為![]() ),點
),點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上.
上.
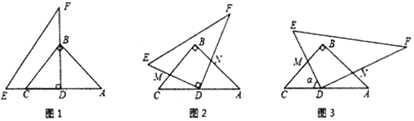
(1)求重疊部分![]() 的面積;
的面積;
(2)如圖2,將直角三角板![]() 繞
繞![]() 點按順時針方向旋轉30度,
點按順時針方向旋轉30度,![]() 交
交![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() .
.
①請說明:![]() ;
;
②在此條件下,![]() 與直角三角板
與直角三角板![]() 重疊部分的面積會發生變化嗎?請說明理由,并求出重疊部分的面積.
重疊部分的面積會發生變化嗎?請說明理由,并求出重疊部分的面積.
(3)如圖3,將直角三角板![]() 繞
繞![]() 點按順時針方向旋轉
點按順時針方向旋轉![]() 度(
度(![]() ),
),![]() 交
交![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,則
,則![]() 的結論仍成立嗎?重疊部分的面積會變嗎?(請直接寫出結論,不需要說明理由)
的結論仍成立嗎?重疊部分的面積會變嗎?(請直接寫出結論,不需要說明理由)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com