
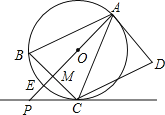
【題目】如圖,AD是![]() 的切線,切點為A,AB是
的切線,切點為A,AB是![]() 的弦,過點B作
的弦,過點B作![]() ,交
,交![]() 于點C,連接AC,過點C作
于點C,連接AC,過點C作![]() ,交AD于點D,連接AO并延長AO交BC于點M,交
,交AD于點D,連接AO并延長AO交BC于點M,交![]() 于點E,交過點C的直線于點P,且
于點E,交過點C的直線于點P,且![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 判斷直線PC與
判斷直線PC與![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
![]() 若
若![]() ,
,![]() ,求PC的長.
,求PC的長.
【答案】(1)證明見解析;(2)![]() 與圓O相切,理由見解析.(3)
與圓O相切,理由見解析.(3)![]()
【解析】分析:(1)由AD是⊙O的切線,BC∥AD,易得AO⊥BC,然后由垂徑定理求得![]() ,繼而證得結論;
,繼而證得結論;
(2)過C點作直徑CF,連接FB,由CF為直徑得∠F+∠BCE=90°,由AB∥DC得∠ACD=∠BAC,而∠BAC=∠F,∠BCP=∠ACD,所以∠F=∠BCP,于是∠BCP+∠BCF=90°,然后根據切線的判斷得到結論;
(3)根據切線的性質得到OA⊥AD,而BC∥AD,則AM⊥BC,根據垂徑定理求得BM與CM的長,根據等腰三角形性質有AC=AB=9,在Rt△AMC中根據勾股定理計算出AM=6![]() ,設⊙O的半徑為r,則OC=r,OM=AM-r=6
,設⊙O的半徑為r,則OC=r,OM=AM-r=6![]() -r,在Rt△OCM中,根據勾股定理計算出r的值即可.
-r,在Rt△OCM中,根據勾股定理計算出r的值即可.
詳解:![]() 證明:
證明:![]() 是
是![]() 的切線,
的切線,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 與圓O相切,理由為:
與圓O相切,理由為:
解:過C點作直徑CF,連接FB,如圖,
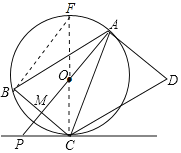
![]() 為直徑,
為直徑,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() 與圓O相切;
與圓O相切;
![]() 解:
解:![]() 是
是![]() 的切線,切點為A
的切線,切點為A
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
設![]() 的半徑為r,則
的半徑為r,則![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() :
:![]() :FB,
:FB,
![]() ,
,
![]() .
.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 的三個頂點的坐標分別為
的三個頂點的坐標分別為![]() ,
,![]() ,
,![]() .
.
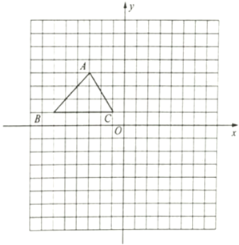
(1)畫出![]() 關于原點中心對稱的
關于原點中心對稱的![]() ,其中A,B,C的對應點分別為
,其中A,B,C的對應點分別為![]() ,
,![]() ,
,![]() ;
;
(2)在(1)的基礎上,將![]() 向上平移4個單位長度,畫出平移后的
向上平移4個單位長度,畫出平移后的![]() ,并寫出
,并寫出![]() 的對應點
的對應點![]() 的坐標;
的坐標;
(3)D為y軸上一點,且![]() 是以AB為直角邊的直角三角形.請直接寫出D點的坐標.
是以AB為直角邊的直角三角形.請直接寫出D點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一個形如六邊形的點陣,它的中心是一個點,算做第一層,第二層每邊兩個點,第三層每邊三個點,以此類推.

(1)填寫下表:
層數 |
|
|
|
|
|
該層對應的點數 |
|
|
| ________ | ________ |
(2)寫出第![]() 層對應的點數(
層對應的點數(![]() );
);
查看答案和解析>>
科目:初中數學 來源: 題型:
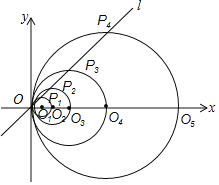
【題目】如圖,在平面直角坐標系中,直線l的函數表達式為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,以
,以![]() 為圓心,
為圓心,![]() 為半徑畫圓,交直線l于點
為半徑畫圓,交直線l于點![]() ,交x軸正半軸于點
,交x軸正半軸于點![]() ,以
,以![]() 為圓心,
為圓心,![]() 為半徑畫圓,交直線l于點
為半徑畫圓,交直線l于點![]() ,交x軸正半軸于點
,交x軸正半軸于點![]() ,以
,以![]() 為圓心,
為圓心,![]() 為半徑畫圓,交直線l于點
為半徑畫圓,交直線l于點![]() ,交x軸正半軸于點
,交x軸正半軸于點![]() ;
;![]() 按此做法進行下去,其中
按此做法進行下去,其中![]() 的長為______.
的長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自行車廠一周計劃生產1400輛自行車,平均每天生產200輛,由于各種原因實際每天生產量與計劃量相比有出入.下表是某周的生產情況(超產為正、減產為負):
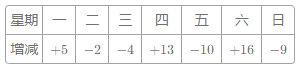
(1)產量最多的一天比產量最少的一天多生產 輛?
(2)該廠實行每周計件工資制,每生產一輛車可得60元,若超額完成任務,則超過部分每輛另獎20元,少生產一輛扣15元,那么該廠工人這一周的工資總額是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在市舉辦的“劃龍舟,慶端午”比賽中,甲、乙兩隊在比賽時的路程![]() (米)與時間
(米)與時間![]() (分鐘)之間的函數關系圖象如圖所示,根據圖象得到下列結論,你認為正確的結論是( )
(分鐘)之間的函數關系圖象如圖所示,根據圖象得到下列結論,你認為正確的結論是( )
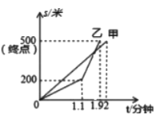
①這次比賽的全程是![]() 米;②乙隊先到達終點;③比賽中兩隊從出發到
米;②乙隊先到達終點;③比賽中兩隊從出發到![]() 分鐘時間段,乙隊的速度比甲隊的速度快;④乙與甲相遇時乙的速度是
分鐘時間段,乙隊的速度比甲隊的速度快;④乙與甲相遇時乙的速度是![]() 米/分鐘;⑤在
米/分鐘;⑤在![]() 分鐘時,乙隊追上了甲隊.
分鐘時,乙隊追上了甲隊.
A.①③④B.①②⑤C.①②④D.①②③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠B=30°,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N,再分別以M、N為圓心,大于![]() MN的長為半徑畫弧,兩弧交于點P,連結AP并延長交BC于點D,則下列說法中正確的個數是( )
MN的長為半徑畫弧,兩弧交于點P,連結AP并延長交BC于點D,則下列說法中正確的個數是( )
①AD是∠BAC的平分線;②∠ADC=60°;③點D在AB的中垂線上;④S△DAC:S△ABC=1:3.
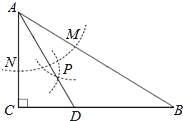
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
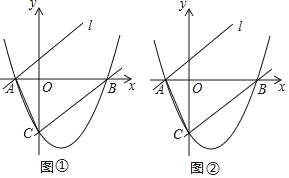
【題目】如圖所示,拋物線y=![]() ﹣
﹣![]() x﹣4與x軸交于點A、B,與y 軸相交于點C.
x﹣4與x軸交于點A、B,與y 軸相交于點C.
(1)求直線BC的解析式;
(2)將直線BC向上平移后經過點A得到直線l:y=mx+n,點D在直線l上,若以A、B、C、D為頂點的四邊形是平行四邊形,求出點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,以AB為直徑的⊙O分別與BC、AC交于點D、E,過點D作⊙O的切線DF,交AC于點F.
(1)求證:DF⊥AC;
(2)若⊙O的半徑為4,∠CDF=22.5°,求陰影部分的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com