
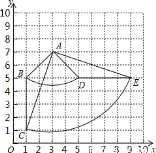
如圖,在10×10的正方形網格中(每個小正方形的邊長都為1個單位),△ 的三個頂點都在格點上.
的三個頂點都在格點上.
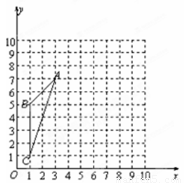
(1)建立如圖所示的直角坐標系,請在圖中標出△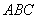 的外接圓的圓心
的外接圓的圓心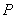 的位置,并填寫:
的位置,并填寫:
①圓心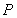 的坐標:
的坐標: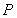 (_______,_______);
(_______,_______);
②⊙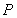 的半徑為_______ .
的半徑為_______ .
(2)將△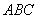 繞點
繞點 逆時針旋轉
逆時針旋轉 得到△
得到△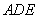 ,畫出圖形,并求線段
,畫出圖形,并求線段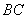 掃過的圖形的面積.
掃過的圖形的面積.
(1)(5,3),2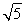 ;(2)8π.
;(2)8π.
【解析】
試題分析:(1)利用外接圓的作法得出P點坐標,進而求出外接圓的半徑即可;
(2)根據勾股定理求出AC,根據旋轉推出△ABC的面積等于△ADE的面積,根據線段BC掃過的圖形的面積=S扇形ACE+S△ABC﹣S扇形ABD﹣S△ADE,根據扇形和三角形的面積公式代入求出即可.
試題解析:(1)如圖所示:
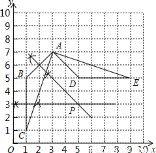
①圓心P的坐標:P(5,3);
②⊙P的半徑為: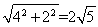 ,
,
故答案為:(5,3),2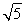 ;
;
(2)∵由勾股定理得:AC=2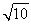 ,AB=2
,AB=2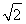 ,
,
∵將△ABC繞點A逆時針旋轉90°得到△ADE,
∴線段BC掃過的圖形的面積=S扇形ACE+S△ABC﹣S扇形ABD﹣S△ADE
=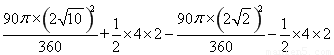 =8π.
=8π.
 .
.
考點:旋轉變換.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
 如圖,在10×10的方格紙中,有一格點三角形ABC.(說明:頂點都在網格線交點處的三角形叫做格點三角形)
如圖,在10×10的方格紙中,有一格點三角形ABC.(說明:頂點都在網格線交點處的三角形叫做格點三角形)查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 2 |
| 3 | 4 |
| 文具 | 計算器 |
| 計算器 | 海寶 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 形頂點上,且點A與原點重合.
形頂點上,且點A與原點重合.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2009•濱湖區一模)如圖,在10×10的正方形網格中(每個小正方形的邊長都為1個單位),△ABC的三個頂點都在格點上.
(2009•濱湖區一模)如圖,在10×10的正方形網格中(每個小正方形的邊長都為1個單位),△ABC的三個頂點都在格點上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在10×10的正方形網格中(每個小正方形的邊長都為1個單位),△ABC的三個頂點都在格點上.
如圖,在10×10的正方形網格中(每個小正方形的邊長都為1個單位),△ABC的三個頂點都在格點上.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com