【題目】中國“蛟龍”號深潛器目前最大深潛極限為7062．68米．某天該深潛器在海面下1800米處作業(yè)（如圖），測得正前方海底沉船C的俯角為45°，該深潛器在同一深度向正前方直線航行2000米到B點，此時測得海底沉船C的俯角為60°．請判斷沉船C是否在“蛟龍”號深潛極限范圍內(nèi)？并說明理由；（精確到0．01）（參考數(shù)據(jù)：
≈1．414，
≈1．732）
【答案】在，理由見解析．
【解析】
試題分析：過點C作CD垂直AB延長線于點D，設(shè)CD為x米，在Rt△ACD和Rt△BCD中，分別表示出AD和BD的長度，然后根據(jù)AB=2000米，求出x的值，求出點C距離海面的距離，判斷是否在極限范圍內(nèi)；
試題解析：過點C作CD垂直AB延長線于點D，
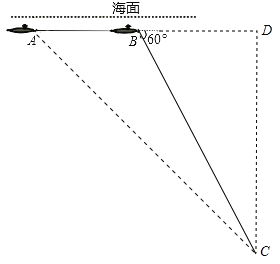
設(shè)CD=x米，
在Rt△ACD中，
∵∠DAC=45°，
∴AD=x，
在Rt△BCD中，
∵∠CBD=60°，
∴BD=
，
∴AB=AD-BD=x- =2000，
解得：x≈4732，
∴船C距離海平面為4732+1800=6532米＜7062．68米，
∴沉船C在“蛟龍”號深潛極限范圍內(nèi)；
科目：初中數(shù)學(xué) 來源： 題型：
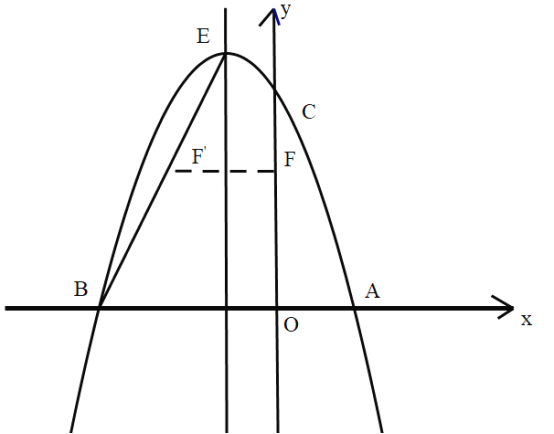
【題目】如圖，二次函數(shù)
的圖像與
軸交于
兩點，與
軸交于點
，直線l是拋物線的對稱軸，
是拋物線的頂點．
(1)求拋物線的解析式及頂點的坐標(biāo)；
(2)如圖，連接
，線段
上的點
關(guān)于直線
的對稱點
恰好在線段上，求點的坐標(biāo)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
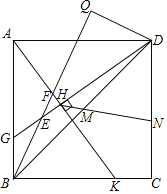
【題目】如圖，Q為正方形ABCD外一點，連接BQ，過點D作DQ⊥BQ，垂足為Q，G、K分別為AB、BC上的點，連接AK、DG，分別交BQ于F、E，AK⊥DG，垂足為點H，AF＝5，DH＝8，F為BQ中點，M為對角線BD的中點，連接HM并延長交正方形于點N，則HN的長為_____．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】拋物線
交
軸于點
，
，交
軸的負(fù)半軸于
，頂點為
．下列結(jié)論：①
；②
；③當(dāng)
時，
；④當(dāng)
是等腰直角三角形時，則
；⑤若
，
是一元二次方程
的兩個根，且
，則
．其中錯誤的有（ ）個．
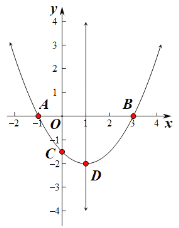
A.5B.4C.3D.2
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】已知某商品的進(jìn)價為每件40元．現(xiàn)在的售價是每件60元．每星期可賣出300件．市場調(diào)查反映：如調(diào)整價格，每漲價一元．每星期要少賣出10件；每降價一元，每星期可多賣出18件．如何定價才能使利潤最大？
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，
是一張放在平面直角坐標(biāo)系中的紙片，點
與原點
重合，點
在
軸的正半軸上，點
在
軸的正半軸上．已知
，
．將紙片的直角部分翻折，使點落在
邊上，記為點
，
為折痕，點
在軸上．
（1）在如圖所示的直角坐標(biāo)系中，點的坐標(biāo)為，________，
________；
（2）線段
上有一動點
（不與點，重合）自點沿方向以每秒
個單位長度向點做勻速運動，設(shè)運動時間為
，過點作
交于點
，過點作
交
于點
，求四邊形
的面積
與時間
之間的函數(shù)表達(dá)式．當(dāng)取何值時，有最大值？最大值是多少？
（3）當(dāng)為何值時，，，三點構(gòu)成一個等腰三角形？并求出點的坐標(biāo)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知拋物線
與
軸交于點
．
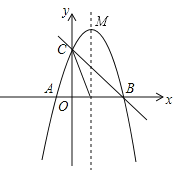
（1）求該拋物線的表達(dá)式；
（2）點
是線段
上方的拋物線上一個動點，求
的面積的最大值；
（3）點
是拋物線的對稱軸上一個動點，當(dāng)以
為頂點的三角形是直角三角形時，求出點的坐標(biāo)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】【題目】如圖①，一次函數(shù) y＝
x - 2 的圖像交 x 軸于點 A，交 y 軸于點 B，二次函數(shù) y＝
x2 bx c的圖像經(jīng)過 A、B 兩點，與 x 軸交于另一點 C．
（1）求二次函數(shù)的關(guān)系式及點 C 的坐標(biāo)；
（2）如圖②，若點 P 是直線 AB 上方的拋物線上一點，過點 P 作 PD∥x 軸交 AB 于點 D，PE∥y 軸交 AB 于點 E，求 PD＋PE 的最大值；
（3）如圖③，若點 M 在拋物線的對稱軸上，且∠AMB＝∠ACB，求出所有滿足條件的點 M的坐標(biāo)．
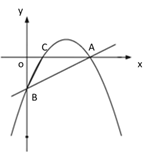
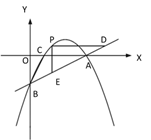
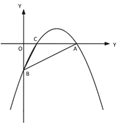
① ② ③
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】我市某鄉(xiāng)鎮(zhèn)在“精準(zhǔn)扶貧”活動中銷售農(nóng)產(chǎn)品，經(jīng)分析發(fā)現(xiàn)月銷售量
(萬件與月份
(月)的關(guān)系為: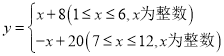
每件產(chǎn)品的利潤
(元)與月份(月)的關(guān)系如下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
請你根據(jù)表格直接寫出每件產(chǎn)品利潤z (元) 與月份(月)的函數(shù)關(guān)系式;
若月利潤
(萬元) =當(dāng)月銷售量(萬件) 當(dāng)月每件產(chǎn)品的利潤(元)，求月利潤(萬元)與月份(月)的關(guān)系式;
當(dāng)為何值時，月利潤有最大值，最大值為多少?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com