
【題目】在平面直角坐標系![]() 中,
中,![]() 、
、![]() 為平面內不重合的兩個點,若
為平面內不重合的兩個點,若![]() 到
到![]() 、
、![]() 兩點的距離相等,則稱點
兩點的距離相等,則稱點![]() 是線段
是線段![]() 的“似中點”.
的“似中點”.
(1)已知![]() ,
,![]() , 在點
, 在點![]() 、
、![]() 、
、![]() 、
、![]() 中,線段
中,線段![]() 的“似中點”是點 .
的“似中點”是點 .
(2)直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
①若點![]() 是線段
是線段![]() 的“似中點”,且在坐標軸.上,求
的“似中點”,且在坐標軸.上,求![]() 點的坐標;
點的坐標;
②若![]() 的半徑為2,圓心
的半徑為2,圓心![]() 為
為![]() ,若
,若![]() 上存在線段
上存在線段![]() 的“似中點”,請直接寫出
的“似中點”,請直接寫出![]() 的取值范圍.
的取值范圍.
【答案】(1)D,F;(2)①(1,0)和(0,![]() );②-3≤t≤5.
);②-3≤t≤5.
【解析】
(1)分別求出點A,B與點C,D,E,F的距離,再根據“似中點”的定義,進行判斷即可;
(2)①由題意得:點H為MN的垂直平分線與坐標軸的交點,畫出圖形,根據含30°角的直角三角形的性質,即可求解;②設點P到H1H2的距離為h,則當h≤2時,![]() 上存在線段
上存在線段![]() 的“似中點”, h=
的“似中點”, h=![]()
![]() ,進而即可求出答案.
,進而即可求出答案.
(1)∵![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴線段![]() 的“似中點”是點D,F.
的“似中點”是點D,F.
故答案是:D,F;
(2)①由題意可知:M(-1,0),N(0,![]() ),
),
∴∠NMO=60°,MN=![]() ,
,
∵點![]() 是線段
是線段![]() 的“似中點”,且在坐標軸上,
的“似中點”,且在坐標軸上,
∴點H為MN的垂直平分線與坐標軸的交點,
∴∠MH1H2=30°,
∴H1M=2,
∴H1(1,0),
∵OH2=![]() OH1=
OH1=![]() ,
,
∴H2(0,![]() ),
),
綜上所述,![]() 點的坐標為:(1,0)和(0,
點的坐標為:(1,0)和(0,![]() );
);
②若![]() 上存在線段
上存在線段![]() 的“似中點”,則
的“似中點”,則![]() 與線段MN的垂直平分線H1H2有公共點.
與線段MN的垂直平分線H1H2有公共點.
設點P到H1H2的距離為h,則當h≤2時,![]() 上存在線段
上存在線段![]() 的“似中點”,
的“似中點”,
∵∠H2H1O=30°,
∴h=![]() H1P=
H1P=![]()
![]() ,
,
∴![]()
![]() ≤2,解得:-3≤t≤5.
≤2,解得:-3≤t≤5.
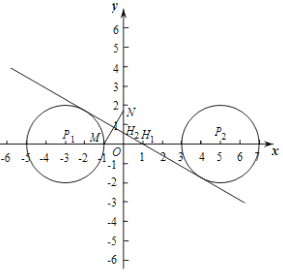


科目:初中數學 來源: 題型:
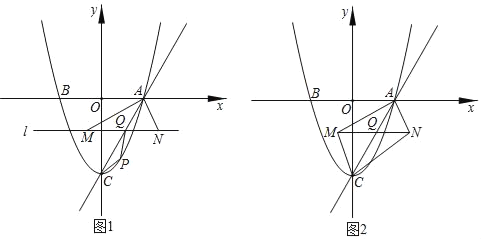
【題目】如圖1,拋物線y=x2﹣3與x軸交于AB兩點(點A在點B的右側),與y軸交于點C,連接AC.點Q是線段AC上的動點,過Q作直線l∥x軸,直線1與∠BAC的平分線交于點M,與∠CAx的平分線交于點N.
(1)P是直線AC下方拋物線上一動點,連接PA,PC,當△PAC的面積最大時,求PQ+![]() AM的最小值;
AM的最小值;
(2)如圖2,連接MC,NC,當四邊形AMCN為矩形時,將△AMN沿著直線AC平移得到△A'M'N',邊A'M'所在的直線與y軸交于D點,若△DM'N'為等腰三角形時,求OD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
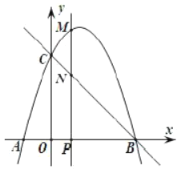
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),點
的左側),點![]() 的坐標為
的坐標為![]() ,與
,與![]() 軸交于點
軸交于點![]() ,作直線
,作直線![]() .動點
.動點![]() 在
在![]() 軸上運動,過點
軸上運動,過點![]() 作
作![]() 軸,交拋物線于點
軸,交拋物線于點![]() ,交直線
,交直線![]() 于點
于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() .
.
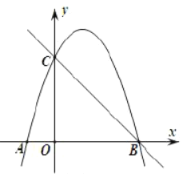
(1)直接寫出拋物線的解析式__________和直線![]() 的解析式_________;
的解析式_________;
(2)當點![]() 在線段
在線段![]() 上運動時,直接寫出線段
上運動時,直接寫出線段![]() 長度的最大值_________;
長度的最大值_________;
(3)當點![]() 在線段
在線段![]() 上運動時,若
上運動時,若![]() 是以
是以![]() 為腰的等腰直角三角形時,求
為腰的等腰直角三角形時,求![]() 的值;
的值;
(4)當以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是平行四邊形時,求出
為頂點的四邊形是平行四邊形時,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】網上購物已經成為人們常用的一種購物方式,售后評價特別引人關注,消費者在網店購買某種商品后,對其有“好評”、“中評”、“差評”三種評價,假設這三種評價是等可能的.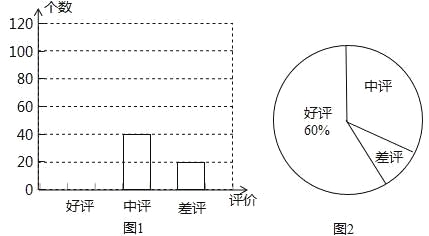
(1)小明對一家網店銷售某種商品顯示的評價信息進行了統計,并列出了兩幅不完整的統計圖.利用圖中所提供的信息解決以下問題:
①小明一共統計了多少個評價;
②請將圖1補充完整;
③求出圖2中“差評”所在扇形圓心角的度數.
(2)若甲、乙兩名消費者在該網店購買了同一商品,請你用列表格或畫樹狀圖的方法幫助店主求一下兩人中至少有一個給“好評”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩位同學進行長跑訓練,甲和乙所跑的路程S(單位:米)與所用時間t(單位:秒)之間的函數圖象分別為線段OA和折線OBCD.則下列說法正確的是( )
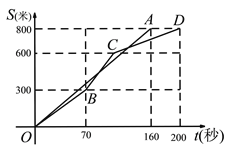
A. 兩人從起跑線同時出發,同時到達終點
B. 跑步過程中,兩人相遇一次
C. 起跑后160秒時,甲、乙兩人相距最遠
D. 乙在跑前300米時,速度最慢
查看答案和解析>>
科目:初中數學 來源: 題型:
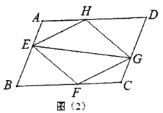
【題目】如圖,在平行四邊形![]() 中,點
中,點![]() ,
,![]() ,
,![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() ,
,![]() ,
,![]() 上,
上,![]() ,
,![]() .
.
(1)如圖(1)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)如圖(2)若![]() 平分
平分![]() ,在不添加輔助線的條件下,直接寫出長度等于
,在不添加輔助線的條件下,直接寫出長度等于![]() 的線段(不包括
的線段(不包括![]() ).
).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,它與x軸的兩個交點分別為(﹣1,0),(3,0).對于下列命題:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正確的有( )
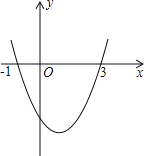
A.3個B.2個C.1個D.0個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知A、B兩地之間的路程為3000m,甲、乙兩人分別從A、B兩地同時出發,相向而行,甲到B地停止,乙到A地停止,出發10分鐘后,甲原路原速返回A地取重要物品,取到該物品后立即原路原速前往B地(取物品的時間忽略不計),結果到達B地的時間比乙到達A地的時間晚,在整個行走過程中,甲、乙兩人均保持各自的速度勻速行走,甲、乙兩人相距的路程y(m)與甲運動的時間x(min)之間的關系如圖所示,則乙到達A地時,甲與B地相距的路程是_____m.
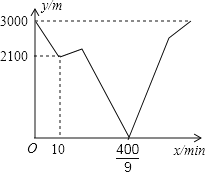
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,水壩的橫截面是梯形![]() ,迎水坡
,迎水坡![]() 的坡角
的坡角![]() 為
為![]() ,背水坡
,背水坡![]() 的坡度
的坡度![]() 為
為![]() ,壩頂寬
,壩頂寬![]() 米,壩高5米.求:
米,壩高5米.求:
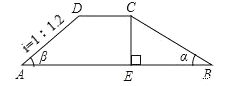
(1)壩底寬![]() 的長(結果保留根號);
的長(結果保留根號);
(2)在上題中,為了提高堤壩的防洪能力,市防汛指揮部決定加固堤壩,要求壩頂![]() 加寬0.5米,背水坡
加寬0.5米,背水坡![]() 的坡度改為
的坡度改為![]() ,已知堤壩的總長度為
,已知堤壩的總長度為![]() ,求完成該項工程所需的土方(結果保留根號).
,求完成該項工程所需的土方(結果保留根號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com