【答案】
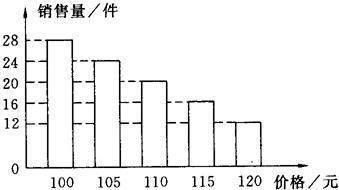
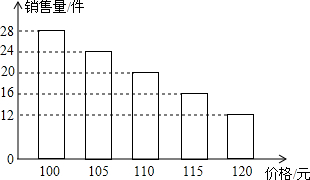
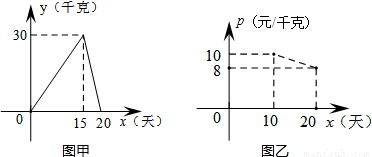
分析:(1)分兩種情況進行討論:①0≤x≤15;②15<x≤20,針對每一種情況,都可以先設出函數的解析式,再將已知點的坐標代入,利用待定系數法求解;
(2)日銷售金額=日銷售單價×日銷售量.由于第10天和第15天在第10天和第20天之間,當10≤x≤20時,設銷售單價p(元/千克)與銷售時間x(天)之間的函數關系式為p=mx+n,由點(10,10),(20,8)在p=mx+n的圖象上,利用待定系數法求得p與x的函數解析式,繼而求得10天與第15天的銷售金額;
(3)日銷售量不低于24千克,即y≥24.先解不等式2x≥24,得x≥12,再解不等式-6x+120≥24,得x≤16,則求出“最佳銷售期”共有5天;然后根據p=-

x+12(10≤x≤20),利用一次函數的性質,即可求出在此期間銷售時單價的最高值.
解答:解:(1)分兩種情況:
①當0≤x≤15時,設日銷售量y與銷售時間x的函數解析式為y=k
1x,
∵直線y=k
1x過點(15,30),
∴15k
1=30,解得k
1=2,
∴y=2x(0≤x≤15);
②當15<x≤20時,設日銷售量y與銷售時間x的函數解析式為y=k
2x+b,
∵點(15,30),(20,0)在y=k
2x+b的圖象上,
∴
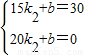
,解得:

,
∴y=-6x+120(15<x≤20);
綜上,可知y與x之間的函數關系式為:
y=
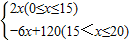
;
(2)∵第10天和第15天在第10天和第20天之間,
∴當10≤x≤20時,設銷售單價p(元/千克)與銷售時間x(天)之間的函數解析式為p=mx+n,
∵點(10,10),(20,8)在z=mx+n的圖象上,
∴
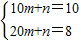
,解得:
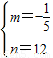
,
∴p=-

x+12(10≤x≤20),
當x=10時,p=10,y=2×10=20,銷售金額為:10×20=200(元),
當x=15時,p=-

×15+12=9,y=30,銷售金額為:9×30=270(元).
故第10天和第15天的銷售金額分別為200元,270元;
(3)若日銷售量不低于24千克,則y≥24.
當0≤x≤15時,y=2x,
解不等式2x≥24,得x≥12;
當15<x≤20時,y=-6x+120,
解不等式-6x+120≥24,得x≤16,
∴12≤x≤16,
∴“最佳銷售期”共有:16-12+1=5(天);
∵p=-

x+12(10≤x≤20),-

<0,
∴p隨x的增大而減小,
∴當12≤x≤16時,x取12時,p有最大值,此時p=-

×12+12=9.6(元/千克).
故此次銷售過程中“最佳銷售期”共有5天,在此期間銷售單價最高為9.6元.
點評:此題考查了一次函數的應用,有一定難度.解題的關鍵是理解題意,利用待定系數法求得函數解析式,注意數形結合思想與函數思想的應用.

 x+12(10≤x≤20),利用一次函數的性質,即可求出在此期間銷售時單價的最高值.
x+12(10≤x≤20),利用一次函數的性質,即可求出在此期間銷售時單價的最高值.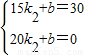 ,解得:
,解得: ,
,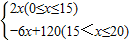 ;
;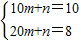 ,解得:
,解得: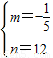 ,
, x+12(10≤x≤20),
x+12(10≤x≤20), ×15+12=9,y=30,銷售金額為:9×30=270(元).
×15+12=9,y=30,銷售金額為:9×30=270(元). x+12(10≤x≤20),-
x+12(10≤x≤20),- <0,
<0, ×12+12=9.6(元/千克).
×12+12=9.6(元/千克).

 名校課堂系列答案
名校課堂系列答案