
 3)是反比例函數圖象上的點:
3)是反比例函數圖象上的點: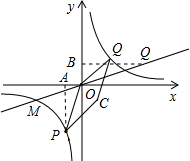 解:(1)設正比例函數解析式為y=kx,將點M坐標代入得
解:(1)設正比例函數解析式為y=kx,將點M坐標代入得 ,
, ;
; .
.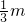 ),
), |OB•BQ|=
|OB•BQ|= ×|
×| m•m|=
m•m|=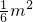 ,
, ×1×3=
×1×3= ,
,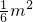 =
= ,解得:m=±3,所以點Q的坐標為Q1(3,1)和Q2(-3,-1).
,解得:m=±3,所以點Q的坐標為Q1(3,1)和Q2(-3,-1).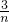 ),
),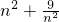 .
.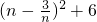 ,當
,當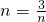 即
即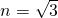 時,OQ2有最小值6,這時Q(
時,OQ2有最小值6,這時Q( ,
, ),
), .
. ,所以平行四邊形OPCQ周長的最小值是
,所以平行四邊形OPCQ周長的最小值是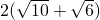 .
.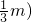 ,由△OBQ與△OAP面積相等,可得關系式,進而可得m的值,代入可得Q1與Q2的坐標;
,由△OBQ與△OAP面積相等,可得關系式,進而可得m的值,代入可得Q1與Q2的坐標;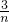 ),分析可得求□OPCQ周長的最小值就只需求OQ的最小值,進而可得OQ的二次關系式,解可得答案.
),分析可得求□OPCQ周長的最小值就只需求OQ的最小值,進而可得OQ的二次關系式,解可得答案.

 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:
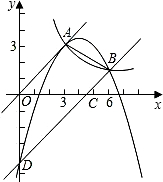 邊形OABD的面積S滿足:S1=
邊形OABD的面積S滿足:S1=| 2 | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
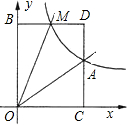 如圖,已知正比例函數y=ax與反比例函數y=
如圖,已知正比例函數y=ax與反比例函數y=| k | x |
查看答案和解析>>
科目:初中數學 來源: 題型:
| k | x |
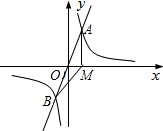 標為1,過點A作x軸的垂線,垂足為M,連接BM.
標為1,過點A作x軸的垂線,垂足為M,連接BM.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知正比例函數y=kx的圖象經過點A(-2
如圖,已知正比例函數y=kx的圖象經過點A(-2| 3 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知正比例函數和反比例函數的圖象都經過點A(3,3).
如圖,已知正比例函數和反比例函數的圖象都經過點A(3,3).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com