
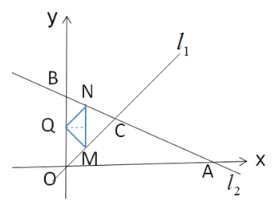
【題目】如圖,在平面直角坐標系中,直線![]() 的解析式為
的解析式為![]() ,直線
,直線![]() 的解析式為
的解析式為![]() ,與
,與![]() 軸,
軸,![]() 軸分別交于點
軸分別交于點![]() ,點
,點![]() ,直線
,直線![]() 與
與![]() 交于點
交于點![]() .
.

(1)求點![]() ,點
,點![]() ,點
,點![]() 的坐標,并求出
的坐標,并求出![]() 的面積;
的面積;
(2)若直線 ![]() 上存在點
上存在點![]() (不與
(不與![]() 重合),滿足
重合),滿足![]() ,請求出點
,請求出點![]() 的坐標;
的坐標;
(3)在![]() 軸右側有一動直線平行于
軸右側有一動直線平行于![]() 軸,分別與
軸,分別與![]() ,
,![]() 交于點
交于點![]() ,且點
,且點![]() 在點
在點![]() 的下方,
的下方,![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() 為等腰直角三角形?若存在,請直接寫出滿足條件的點
為等腰直角三角形?若存在,請直接寫出滿足條件的點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,點
;(3)存在,點![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]() .
.
【解析】
(1)把![]() 和
和![]() 分別代入
分別代入![]() 可求出點
可求出點![]() ,點
,點![]() 坐標,聯立直線
坐標,聯立直線![]() 和直線
和直線![]() 解析式可求得點
解析式可求得點![]() 的坐標,然后根據B,C坐標可求
的坐標,然后根據B,C坐標可求![]() 的面積;
的面積;
(2)作![]() 軸于點
軸于點![]() ,
,![]() 軸于點E,根據
軸于點E,根據![]() 可得
可得![]() ,代入
,代入![]() 的解析式
的解析式![]() 可求出點
可求出點![]() 的坐標;
的坐標;
(3)分情況討論:①當![]() 時,②當
時,②當![]() 時,③當
時,③當![]() 時,分別求出點
時,分別求出點![]() 的坐標即可.
的坐標即可.
解:(1)把![]() 代入
代入![]() 可得
可得![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() 可得
可得![]() ,
,
∴![]() ,
,
聯立直線![]() 和直線
和直線![]() 得:
得: ,解得:
,解得:![]() ,
,
∴![]() 點坐標為
點坐標為![]() ,
,
∵ ![]() ,
, ![]() ,
,
∴![]() ;
;
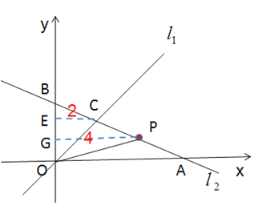
(2)作![]() 軸于點
軸于點![]() ,
,![]() 軸于點E,
軸于點E,
∵![]()
∴![]()
∴![]() ,
,
∴把![]() 代入
代入![]() 的解析式
的解析式![]() ,得
,得![]() ,
,
∴![]() 存在點
存在點![]() 滿足
滿足![]() ;
;
(3)點![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]() ,
,
設動直線為![]() ,由題可得
,由題可得![]() ,
,
則點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,
,
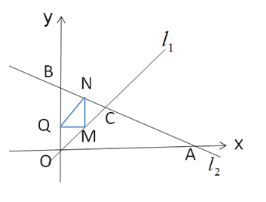
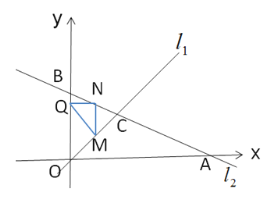
∴![]() (如圖).
(如圖).
①當![]() 時,有
時,有![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴點![]() 的坐標為
的坐標為![]() .
.
∵![]() 軸,
軸,
∴點![]() 的坐標為
的坐標為![]() ;
;
②當![]() 時,有
時,有![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴點![]() 的坐標為
的坐標為![]() .
.
∵![]() 軸,
軸,
∴點![]() 的坐標為
的坐標為![]() ;
;
③當![]() 時,點
時,點![]() 到
到![]() 的距離
的距離![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
∵![]() 為等腰直角三角形,
為等腰直角三角形,
∴點![]() 的坐標為
的坐標為![]() .
.
綜上所述:點![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]() .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,E是正方形ABCD中CD邊上一點,以點A為中心把△ADE順時針旋轉90°。

(1)在圖中畫出旋轉后的圖形;
(2)若旋轉后E點的對應點記為M,點F在BC上,且∠EAF=45°,連接EF。
①求證:△AMF≌△AEF;
②若正方形的邊長為6,AE=![]() ,求EF的長.
,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在Rt△ABC與Rt△OCD中,∠ACB=∠DCO=90°,O為AB的中點.
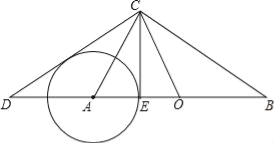
(1)求證:∠B=∠ACD.
(2)已知點E在AB上,且BC2=ABBE.
(i)若tan∠ACD=![]() ,BC=10,求CE的長;
,BC=10,求CE的長;
(ii)試判定CD與以A為圓心、AE為半徑的⊙A的位置關系,并請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,AB=AC,∠B=50°,P 是邊 AB 上的一個動點(不與頂點 A 重合),則∠BPC 的度數可能是

A. 50° B. 80° C. 100° D. 130°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC,以AB為直徑的⊙O交AC于點D,DE⊥BC,垂足為E.

(1)求證:DE是⊙O的切線;
(2)若DG⊥AB,垂足為點F,交⊙O于點G,∠A=35°,⊙O半徑為5,求劣弧DG的長.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=x2+bx+c經過A、B兩點,A、B兩點的坐標分別為(﹣1,0)、(0,﹣3).
(1)求拋物線的函數解析式.
(2)點E為拋物線的頂點,點C為拋物線與x軸的另一交點,點D為y軸上一點,且DC=DE,求出點D的坐標.
(3)在第二問的條件下,射線DE上是否存在點P,使得以C、D、P為頂點的三角形與△DOC相似?若存在,求出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=x+4的圖象與二次函數y=ax(x﹣2)的圖象相交于A(﹣1,b)和B,點P是線段AB上的動點(不與A、B重合),過點P作PC⊥x軸,與二次函數y=ax(x﹣2)的圖象交于點C.

(1)求a、b的值
(2)求線段PC長的最大值;
(3)若△PAC為直角三角形,請直接寫出點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com