
【題目】下表是某網(wǎng)約車公司的專車計(jì)價(jià)規(guī)則.
計(jì)費(fèi)項(xiàng)目 | 起租價(jià) | 里程費(fèi) | 時(shí)長費(fèi) | 遠(yuǎn)途費(fèi) |
單價(jià) | 15元 | 2.5元/公里 | 1.5元/分 | 1元/公里 |
注:車費(fèi)由起租價(jià)、里程費(fèi)、時(shí)長費(fèi)、遠(yuǎn)途費(fèi)四部分構(gòu)成,其中起租價(jià)15元含10分鐘時(shí)長費(fèi)和5公里里程費(fèi),遠(yuǎn)途費(fèi)的收取方式為:行車?yán)锍?/span>10公里以內(nèi)(含10公里)不收遠(yuǎn)途費(fèi),超過10公里的,超出部分每公里收1元.
(1)若小李乘坐專車,行車?yán)锍虨?/span>20公里,行車時(shí)間為30分,則需付車費(fèi)_______元.
(2)若小李乘坐專車,行車?yán)锍虨?/span>![]() 公里,平均時(shí)速為
公里,平均時(shí)速為![]() ,則小李應(yīng)付車費(fèi)多少元? (用含
,則小李應(yīng)付車費(fèi)多少元? (用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(3)小李與小王各自乘坐專車,行車車費(fèi)之和為76元,里程之和為15公里(其中小王的行車?yán)锍滩怀^5公里).如果行駛時(shí)間均為 20分鐘,那么這兩輛專車此次的行駛路程各為多少公里?
【答案】(1)92.5元;(2)小李應(yīng)付車費(fèi)![]() 元;(3)小王和小李乘坐的這兩輛專車此次的行駛路程分別為4公里和11公里.
元;(3)小王和小李乘坐的這兩輛專車此次的行駛路程分別為4公里和11公里.
【解析】
(1)根據(jù)題意分別算出起租價(jià)、里程費(fèi)、時(shí)長費(fèi)和遠(yuǎn)途費(fèi),相加即可得出答案;
(2)先計(jì)算小李乘坐專車的時(shí)長,再計(jì)算出里程費(fèi)和時(shí)長費(fèi),最后再加上起租價(jià)計(jì)算即可得出答案;
(3)先分別設(shè)出小王和小李的里程,再根據(jù)“行車車費(fèi)之和為76元”列出等式,解方程即可得出答案.
解:(1)根據(jù)題意可得:15+(20-5)×2.5+10×1+(30-10)×1.5=92.5(元)
∴需付車費(fèi)92.5元.
(2) ∵![]() , 平均時(shí)速為
, 平均時(shí)速為![]()
小李乘坐專車的時(shí)間為:![]() (分鐘)
(分鐘)
則小李應(yīng)付車費(fèi)為:![]() .
.
![]() 元,
元,
答:小李應(yīng)付車費(fèi)![]() 元.
元.
(3)設(shè)小王的行車?yán)锍虨?/span>![]() 公里,則小李的行車?yán)锍虨?/span>
公里,則小李的行車?yán)锍虨?/span>![]() 公里.
公里.
∵小王的行車?yán)锍滩怀^5公里,且小王、小李行車?yán)锍讨蜑?/span>15公里
∴![]()
依題意有:
![]()
解得:![]() , 且合乎題意
, 且合乎題意
∴小李行車?yán)锍虨?/span>![]() 公里
公里
答:小王和小李乘坐的這兩輛專車此次的行駛路程分別為4公里和11公里.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在正方形![]() 中,連接
中,連接![]() ,
,![]() 為射線
為射線![]() 上的一個(gè)動(dòng)點(diǎn)(與點(diǎn)
上的一個(gè)動(dòng)點(diǎn)(與點(diǎn)![]() 不重合),連接
不重合),連接![]() ,
,![]() 的垂直平分線交線段
的垂直平分線交線段![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() ,
,![]() .
.
提出問題:當(dāng)點(diǎn)![]() 運(yùn)動(dòng)時(shí),
運(yùn)動(dòng)時(shí),![]() 的度數(shù)是否發(fā)生改變?
的度數(shù)是否發(fā)生改變?
探究問題:
(1)首先考察點(diǎn)![]() 的兩個(gè)特殊位置:
的兩個(gè)特殊位置:
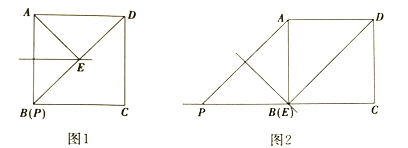
①當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí),如圖1所示,
重合時(shí),如圖1所示,![]() ____________
____________![]()
②當(dāng)![]() 時(shí),如圖2所示,①中的結(jié)論是否發(fā)生變化?直接寫出你的結(jié)論:__________;(填“變化”或“不變化”)
時(shí),如圖2所示,①中的結(jié)論是否發(fā)生變化?直接寫出你的結(jié)論:__________;(填“變化”或“不變化”)
(2)然后考察點(diǎn)![]() 的一般位置:依題意補(bǔ)全圖3,圖4,通過觀察、測量,發(fā)現(xiàn):(1)中①的結(jié)論在一般情況下_________;(填“成立”或“不成立”)
的一般位置:依題意補(bǔ)全圖3,圖4,通過觀察、測量,發(fā)現(xiàn):(1)中①的結(jié)論在一般情況下_________;(填“成立”或“不成立”)
(3)證明猜想:若(1)中①的結(jié)論在一般情況下成立,請從圖3和圖4中任選一個(gè)進(jìn)行證明;若不成立,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 在 數(shù)軸上對應(yīng)的數(shù)分別用
在 數(shù)軸上對應(yīng)的數(shù)分別用![]() 表示,且
表示,且![]() .
.![]() 是數(shù)軸的一動(dòng)點(diǎn).
是數(shù)軸的一動(dòng)點(diǎn).
⑴在數(shù)軸上標(biāo)出![]() 的位置,并求出
的位置,并求出![]() 之間的距離;
之間的距離;
⑵數(shù)軸上一點(diǎn)![]() 距
距![]() 點(diǎn)24個(gè)單位的長度,其對應(yīng)的數(shù)
點(diǎn)24個(gè)單位的長度,其對應(yīng)的數(shù)![]() 滿足
滿足![]() ,當(dāng)
,當(dāng)![]() 點(diǎn)滿足
點(diǎn)滿足![]() 時(shí),求
時(shí),求![]() 點(diǎn)對應(yīng)的數(shù).
點(diǎn)對應(yīng)的數(shù).
⑶動(dòng)點(diǎn)![]() 從原點(diǎn)開始第一次向左移動(dòng)1個(gè)單位,第二次向右移動(dòng)3個(gè)單位長度,第三次向左移動(dòng)5個(gè)單位長度,第四次向右移動(dòng)7個(gè)單位長度,……點(diǎn)
從原點(diǎn)開始第一次向左移動(dòng)1個(gè)單位,第二次向右移動(dòng)3個(gè)單位長度,第三次向左移動(dòng)5個(gè)單位長度,第四次向右移動(dòng)7個(gè)單位長度,……點(diǎn)![]() 能移動(dòng)到與
能移動(dòng)到與![]() 或
或![]() 重合的位置嗎?若能,請?zhí)骄康趲状我苿?dòng)時(shí)重合;若不能,請說明理由.
重合的位置嗎?若能,請?zhí)骄康趲状我苿?dòng)時(shí)重合;若不能,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某班將買一些乒乓球和乒乓球拍,現(xiàn)了解情況如下:甲、乙兩家商店出售兩種同樣品牌的乒乓球和乒乓球拍.乒乓球拍每副定價(jià)![]() 元,乒乓球每盒定價(jià)
元,乒乓球每盒定價(jià)![]() 元,經(jīng)洽談后,甲店每買一-副球拍贈(zèng)一盒乒乓球,乙店全部按定價(jià)的
元,經(jīng)洽談后,甲店每買一-副球拍贈(zèng)一盒乒乓球,乙店全部按定價(jià)的![]() 折優(yōu)惠.該班需買球拍
折優(yōu)惠.該班需買球拍![]() 副,乒乓球若干盒(不小于
副,乒乓球若干盒(不小于![]() 盒).
盒).
(1)當(dāng)購買乒乓球多少盒時(shí),在兩店購買付款一樣?
(2)如果給你![]() 元,讓你選擇- -家商店去辦這件事,你打算去哪家商店購買?為什么?
元,讓你選擇- -家商店去辦這件事,你打算去哪家商店購買?為什么?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
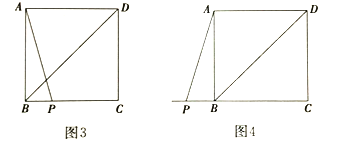
【題目】如圖1,在四邊形ABCD中,如果對角線AC和BD相交并且相等,那么我們把這樣的四邊形稱為等角線四邊形.
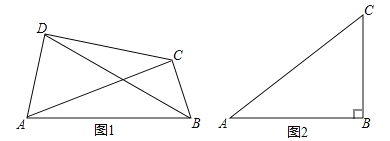
(1)①在“平行四邊形、矩形、菱形”中, 一定是等角線四邊形(填寫圖形名稱);
②若M、N、P、Q分別是等角線四邊形ABCD四邊AB、BC、CD.DA的中點(diǎn),當(dāng)對角線AC、BD還要滿足 時(shí),四邊形MNPQ是正方形.
(2)如圖2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D為平面內(nèi)一點(diǎn).
①若四邊形ABCD是等角線四邊形,且AD=BD,則四邊形ABCD的面積是 ;
②設(shè)點(diǎn)E是以C為圓心,1為半徑的圓上的動(dòng)點(diǎn),若四邊形ABED是等角線四邊形,寫出四邊形ABED面積的最大值,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
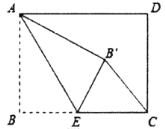
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊上一點(diǎn),連接
邊上一點(diǎn),連接![]() ,把
,把![]() 沿
沿![]() 折疊,使點(diǎn)
折疊,使點(diǎn)![]() 落在點(diǎn)
落在點(diǎn)![]() 處,當(dāng)
處,當(dāng)![]() 為直角三角形時(shí),
為直角三角形時(shí),![]() 的長為( )
的長為( )
A. 3B. ![]() C. 2或3D. 3或
C. 2或3D. 3或![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角坐標(biāo)系中,長方形![]() 的三個(gè)頂點(diǎn)的坐標(biāo)為
的三個(gè)頂點(diǎn)的坐標(biāo)為![]() ,
,![]() ,
,![]() ,且
,且![]() 軸,點(diǎn)
軸,點(diǎn)![]() 是長方形內(nèi)一點(diǎn)(不含邊界).
是長方形內(nèi)一點(diǎn)(不含邊界).

(1)求![]() ,
,![]() 的取值范圍.
的取值范圍.
(2)若將點(diǎn)![]() 向左移動(dòng)8個(gè)單位,再向上移動(dòng)2個(gè)單位到點(diǎn)
向左移動(dòng)8個(gè)單位,再向上移動(dòng)2個(gè)單位到點(diǎn)![]() ,若點(diǎn)
,若點(diǎn)![]() 恰好與點(diǎn)
恰好與點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸對稱,求
軸對稱,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有一種節(jié)能型轎車的油箱加滿天然氣后,油箱中的剩余天然氣量![]() (升)與轎車行駛路程
(升)與轎車行駛路程![]() (千米)之間的關(guān)系如圖所示,根據(jù)圖象回答下列問題:
(千米)之間的關(guān)系如圖所示,根據(jù)圖象回答下列問題:
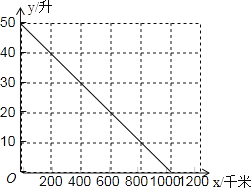
(1)這種轎車的油箱最多能裝______升天然氣,加滿天然氣后可供轎車行駛______千米.
(2)轎車每行駛200千米消耗天然氣________升.
(3)寫出![]() 與
與![]() 之間的函數(shù)關(guān)系式.
之間的函數(shù)關(guān)系式.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com