Question

【題目】如圖，E是△ABC的內心，AE的延長線交△ABC的外接圓于點D.

（1）BD與DE相等嗎？為什么?

（2）若∠BAC=90°，DE=4，求△ABC外接圓的半徑.

Answer 1

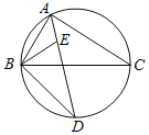
【答案】（1）DE=DB，理由見解析；（2）2

【解析】

(1)由角平分線得出∠ABE=∠CBE，∠BAE=∠CAD，得出弧BD=弧CD,由圓周角定理得出∠DBC=∠CAD,再由三角形的外角性質得出∠DBE=∠DEB,即可得出DE=DB;
(2)由(1)得: 弧BD=弧CD,得出CD=BD=DE=4,由圓周角定理得出BC是直徑, ∠BDC=90°,由勾股定理求出 ,即可得出△ABC外接圓的半徑.

解：（1）DE=DB。

∵AD平分∠BAC，BE平分∠ABC，

∴∠ABE=∠CBE，∠BAE=∠CAD，

∴=，

∴∠DBC=∠CAD，

∴∠DBC=∠BAE，

∵∠DBE=∠CBE+∠DBC，∠DEB=∠ABE+∠BAE，

∴∠DBE=∠DEB，

∴DE=DB；

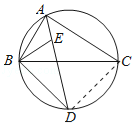
（2）連接CD，如圖所示：由（1）得：=，

∴CD=BD=DE=4，

∵∠BAC=90°，

∴BC是直徑，

∴∠BDC=90°，

∴BC==4，

∴△ABC外接圓的半徑：r=2．