【題目】某市是蜜桔之鄉，今年桔子大豐收，某合作社要把240噸桔子運往某市的A、B兩地，用大、小兩種貨車共20輛，恰好能一次性運完這批桔子，已知這兩種貨車的載重量分別為15噸/輛和10噸/輛．
（1）這兩種貨車各有多少輛？
（2）運往A地的運費為：大車630元/輛，小車420元/輛；運往B地的運費為：大車750元/輛，小車550元/輛．若把20輛貨車中的10輛安排前往A地，其余貨車前往B地，其中調往A地的大車有a輛，求總運費．（用含a的式子表示）
【答案】（1）載重量為15噸/輛的貨車有8輛，載重量為10噸/輛的貨車有12輛；（2）總運費：
（元）.
【解析】
（1）設載重量為15噸/輛的貨車有x輛，載重量為10噸/輛的貨車有y輛，根據兩種車型共20輛且一次可運貨物240噸，即可得出關于x，y的二元一次方程組，解之即可得出結論；
（2）由調往A地的大車有a輛，可得出調往A地的小車有（10﹣a）輛，調往B地的大車有（8﹣a）輛，調往B地的小車有（2+a）輛，根據總運費＝每輛車所需運費×數量，即可用含a的式子表示出總運費．
解：（1）設載重量為15噸/輛的貨車有x輛，載重量為10噸/輛的貨車有y輛，
依題意，得：
，
解得：
．
答：載重量為15噸/輛的貨車有8輛，載重量為10噸/輛的貨車有12輛．
（2）∵調往A地的大車有a輛，
∴調往A地的小車有（10﹣a）輛，調往B地的大車有（8﹣a）輛，調往B地的小車有（2+a）輛，
∴總運費為630a+420（10﹣a）+750（8﹣a）+550（2+a）＝10a+11300（元）．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖1，在矩形ABCD中，E是CB延長線上一個動點，F、G分別為AE、BC的中點，FG與ED相交于點H
(1) 求證：HE＝HG
(2) 如圖2，當BE＝AB時，過點A作AP⊥DE于點P連接BP，求
的值
(3) 在(2)的條件下，若AD＝2，∠ADE＝30°，則BP的長為______________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的一條弦，E是AB的中點，過點E作EC⊥OA于點C，過點B作⊙O的切線交CE的延長線于點D． 
（1）求證：DB=DE；
（2）若AB=12，BD=5，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠BAC的平分線交△ABC的外接圓于點D，∠ABC的平分線交AD于點E， 
（1）求證：DE=DB；
（2）若∠BAC=90°，BD=4，求△ABC外接圓的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB是⊙O的直徑，弦CD與直徑AB相交于點F．點E在⊙O外，做直線AE，且∠EAC=∠D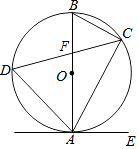 
（1）求證：直線AE是⊙O的切線．
（2）若∠BAC=30°，BC=4，cos∠BAD= 
，CF= 
，求BF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知點
、
，連接
.如果點
在直線
上，且點到直線的距離不大于1，那么稱點是線段的“臨近點”.
（1）判斷點
是否是線段的“臨近點”，并說明理由；
（2）若點
是線段的“臨近點”.①求
的取值范圍；②設直線與
軸交于
點，試用表達
的面積
，并求出的最大面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算：
(1)－a3·a4；
(2) 
2018×
2019.
(3)(－2x2y)3·3(xy2)2；
(4)(－3a＋2b)2
(5)(x－2)(x＋2)(x2＋4)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ABC=90°，∠ACB=30°．將△ABC繞點A按逆時針方向旋轉15°后得到△AB1C1 ， B1C1交AC于點D，如果AD=2 
，則△ABC的周長等于 ．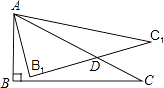 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
