
已知關于x的兩個一元二次方程:
方程①: 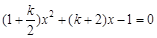 ;方程②:
;方程②: 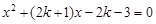 .
.
(1)若方程①有兩個相等的實數根,求解方程②;
(2)若方程①和②中只有一個方程有實數根,請說明此時哪個方程沒有實數根,并化簡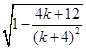 ;
;
(3)若方程①和②有一個公共根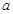 ,求代數式
,求代數式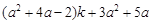 的值.
的值.
(1)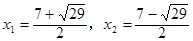 ;(2)
;(2)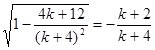 ;(3)5
;(3)5
【解析】
試題分析:(1)根據方程①有兩個相等實數根可得△ ,再結合一元二次方程的二次項系數不為0即可求得k的值,然后再代入方程②求解即可;
,再結合一元二次方程的二次項系數不為0即可求得k的值,然后再代入方程②求解即可;
(2)由方程②得△2=
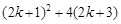 ,再根據
,再根據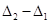
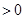 可得
可得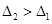 ,由方程①、②只有一個有實數根可得
,由方程①、②只有一個有實數根可得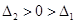 ,即可求得k的取值范圍,再根據二次根式的性質化簡即可;
,即可求得k的取值范圍,再根據二次根式的性質化簡即可;
(3)由a是方程①和②的公共根可得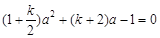 ,
,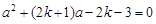 ,即可得到
,即可得到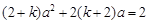 ,
,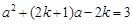 ,從而可以求得結果.
,從而可以求得結果.
解:(1)∵方程①有兩個相等實數根
∴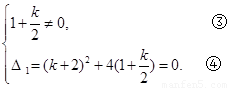
由③得k+2¹0
由④得(k+2)(k+4)=0
∵k+2¹0
∴k=-4
當k=-4時,方程②為: 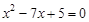 .
.
解得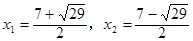 ;
;
(2)由方程②得△2=
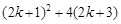 .
.
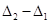 =
=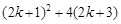 -(k + 2) (k+4) =3k2+6k+5 =3(k+1)2+2>0.
-(k + 2) (k+4) =3k2+6k+5 =3(k+1)2+2>0.
∴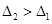 .
.
∵方程①、②只有一個有實數根,
∴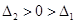
∴此時方程①沒有實數根.
由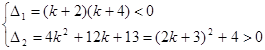
得(k+2)(k+4)<0
 .
.
∵(k+2)(k+4)<0
∴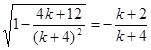 ;
;
(3)∵a是方程①和②的公共根
∴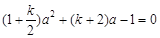 ,
,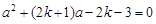
∴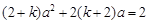 ,
,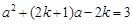
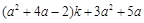
=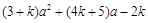
=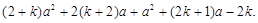
=2+3=5.
考點:一元二次方程根的判別式,解一元二次方程
點評:解題的關鍵是熟練掌握一元二次方程根的情況與判別式△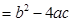 的關系:(1)
的關系:(1)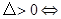 方程有兩個不相等的實數根;(2)
方程有兩個不相等的實數根;(2)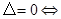 方程有兩個相等的實數根;(3)
方程有兩個相等的實數根;(3)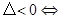 方程沒有實數根.
方程沒有實數根.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
| k |
| 2 |
1-
|
查看答案和解析>>
科目:初中數學 來源: 題型:
| 13 |
| 2 |
| 9 |
| 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:
已知關于x的兩個一元二次方程:
方程①:  ; 方程②:
; 方程②:  .
.
(1)若方程①有兩個相等的實數根,求解方程②;
(2)若方程①和②中只有一個方程有實數根, 請說明此時哪個方程沒有實數根, 并化
簡![]() ;
;
(3)若方程①和②有一個公共根a, 求代數式![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源:2011-2012學年北京市海淀區九年級上學期期中測評數學卷 題型:解答題
已知關于x的兩個一元二次方程:
方程①:  ; 方程②:
; 方程②:  .
.
(1)若方程①有兩個相等的實數根,求解方程②;
(2)若方程①和②中只有一個方程有實數根, 請說明此時哪個方程沒有實數根, 并化
簡 ;
;
(3)若方程①和②有一個公共根a, 求代數式 的值.
的值.
查看答案和解析>>
科目:初中數學 來源:2012屆北京市海淀區九年級上學期期中測評數學卷 題型:解答題
已知關于x的兩個一元二次方程:
方程①:  ; 方程②:
; 方程②:  .
.
(1)若方程①有兩個相等的實數根,求解方程②;
(2)若方程①和②中只有一個方程有實數根, 請說明此時哪個方程沒有實數根, 并化
簡 ;
;
(3)若方程①和②有一個公共根a, 求代數式 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com