
 的圖像過AB的中點D,且和BC相交于點E,F為第一象限的點,AF=12,CF=13.
的圖像過AB的中點D,且和BC相交于點E,F為第一象限的點,AF=12,CF=13. 和直線OE的函數解析式;
和直線OE的函數解析式;
 ,得k=6.
,得k=6. .
.  ,m=
,m=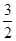 ,
,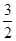 ,4).
,4).  ,將(
,將(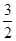 ,4)代入得
,4)代入得
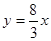 .
.  .
. ,
, 。
。 上,易求點E的橫坐標。
上,易求點E的橫坐標。 是直角三角形需要利用勾股定理逆定理判斷。
是直角三角形需要利用勾股定理逆定理判斷。

 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 軸和
軸和 軸,建立如圖所示的平面直角坐標系.E是邊AC上的一個動點(不與A,C重合),過E點的反比例函數
軸,建立如圖所示的平面直角坐標系.E是邊AC上的一個動點(不與A,C重合),過E點的反比例函數 的圖象與BC邊交于點F.
的圖象與BC邊交于點F. 問當點E運動到什么位置時,S有最大值,其最大值為多少?
問當點E運動到什么位置時,S有最大值,其最大值為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com