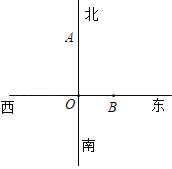
【題目】如圖，一艘貨輪位于O地，發現燈塔A在它的正北方向上，這艘貨輪沿正東方向航行50千米，到達B地，此時用雷達測得燈塔A與貨輪的距離為100千米.
(1)在圖中作出燈塔A的位置，并作射線BA；
(2)以正北，正南方向為基準，借助量角器，描述燈塔A在B地的什么方向上(精確到1°)
中考利劍中考試卷匯編系列答案
教育世家狀元卷系列答案
黃岡課堂作業本系列答案
單元加期末復習先鋒大考卷系列答案科目：初中數學 來源： 題型：
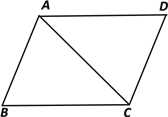
【題目】如圖，已知平行四邊形ABCD中，AC=BC，∠ACB=45°，將三角形ABC沿著AC翻折，點B落在點E處，聯結DE，那么
的值為________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】隨著人們經濟收入的不斷提高，汽車已越來越多地進入到各個家庭．某大型超市為緩解停車難問題，建筑設計師提供了樓頂停車場的設計示意圖．按規定，停車場坡道口上坡要張貼限高標志，以便告知車輛能否安全駛入．如圖，地面所在的直線ME與樓頂所在的直線AC是平行的，CD的厚度為0.5m，求出汽車通過坡道口的限高DF的長（結果精確到0.1m，sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）．
查看答案和解析>>
科目：初中數學 來源： 題型：
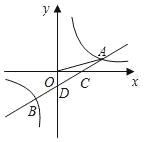
【題目】如圖，一次函數y=ax+b的圖象與反比例函數y=
的圖象交于A，B兩點，與x軸交于點C，與y軸交于點D，已知OA=
，tan∠AOC=
，點B的坐標為（m，﹣2）．
（1）求反比例函數的解析式；
（2）求一次函數的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
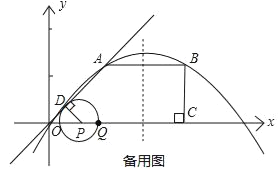
【題目】如圖，O是平面直角坐標系的原點．在四邊形OABC中，AB∥OC，BC⊥x軸于C，A（1，1），B（3，1），動點P從O點出發，沿x軸正方向以2個單位/秒的速度運動．設P點運動的時間為t秒（0＜t＜2）．
（1）求經過O、A、B三點的拋物線的解析式；
（2）過P作PD⊥OA于D，以點P為圓心，PD為半徑作⊙P，⊙P在點P的右側與x軸交于點Q．
①則P點的坐標為_____，Q點的坐標為_____；（用含t的代數式表示）
②試求t為何值時，⊙P與四邊形OABC的兩邊同時相切；
③設△OPD與四邊形OABC重疊的面積為S，請直接寫出S與t的函數解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了了解同學們每月零花錢的數額，校園小記者隨機調查了本校部分同學，根據調查結果，繪制出了如下兩個尚不完整的統計圖表．
調查結果統計表
組別 | 分組（單位：元） | 人數 |
A | 0≤x＜30 | 4 |
B | 30≤x＜60 | 16 |
C | 60≤x＜90 | a |
D | 90≤x＜120 | b |
E | x≥120 | 2 |
請根據以上圖表，解答下列問題：
（1）填空：這次被調查的同學共有__人，a+b=__，m=___；
（2）求扇形統計圖中扇形C的圓心角度數；
（3）該校共有學生1000人，請估計每月零花錢的數額x在60≤x＜120范圍的人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀理解：數和形是數學的兩個主要研究對象，我們經常運用數形結合，樹形轉化的方法解決一些數學問題，小明在求同一坐標軸上兩點間的距離時發現，對于平面直角坐標系內任意兩點P1（x1，y1），P2（x2，y2），可通過構造直角三角形利用圖1得到結論：P1P2=
，他還利用圖2證明了線段P1P2的中點P（x，y），P的坐標公式：x=
，y=
．
啟發應用：
如圖3：在平面直角坐標系中，已知A（8，0），B（0，6），C（1，7），⊙M經過原點O及點A，B，
（1）求⊙M的半徑及圓心M的坐標；
（2）判斷點C與⊙M的位置關系，并說明理由；
（3）若∠BOA的平分線交AB于點N，交⊙M于點E，分別求出OE的表達式y1，過點M的反比例函數的表達式y2，并根據圖象，當y2＞y1＞0時，請直接寫出x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若
的度數是
的度數的k倍，則規定是的k倍角.
（1）若∠M=21°17'，則∠M的5倍角的度數為 ；
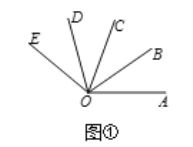
（2）如圖1，OB是∠AOC的平分線，OD是∠COE的平分線，若∠AOC=∠COE，請直接寫出圖中∠AOB的所有3倍角；
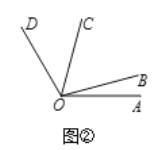
（3）如圖2，若∠AOC是∠AOB的5倍角，∠COD是∠AOB的3倍角，且∠AOC和∠BOD互為補角，求∠AOD的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
