Question

菱形的兩鄰角的度數之比為l：3，邊長為5

2

，則高為

5

．

Answer 1

分析：菱形ABCD的邊長BC=5

2

，CE為高，∠B：∠A=1：3，根據菱形的性質得AD∥BC，則∠A+∠B=180°，可計算出∠B=45°，而CE為高，得到△BCE為等腰直角三角形，根據等腰直角三角形的性質得CE=

2

2

BC，把BC=5

2

代入計算即可．

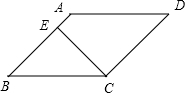
解答：解：如圖，菱形ABCD的邊長BC=5

2

，CE為高，∠B：∠A=1：3，
∵AD∥BC，
∴∠A+∠B=180°，
∴∠B+3∠B=180°，
∴∠B=45°，
而CE為高，
∴△BCE為等腰直角三角形，
∴BC=

2

CE，
∴CE=

2

2

BC=

2

2

×5

2

=5．
故答案為：5．

點評：本題考查了菱形的性質：菱形的對邊分別平行，四條邊都相等，兩條對角線互相垂直平分，并且分別平分兩組內角．也考查了等腰直角三角形的判定與性質．