Question

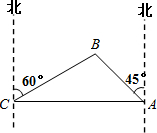
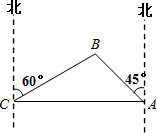
近期南海區域天氣較差，為防止漁民捕撈船只發生意外，我海軍某部奉命在南海海域執行防災救護任務．某天我護漁艦正在某小島A北偏西45°并距該島20海里的B處待命．位于該島正西方向C處的我國一漁船遭到海浪襲擊后船只出現故障，急需要幫助．漁船船長發現在其北偏東60°的方向有我軍護漁艦（如圖所示），便發出緊急求救信號．我護漁艦接警后，立即沿BC航線以每小時60海里的速度前去救援．問護漁艦需多少分鐘可以到達該商船所在的位置C處？（結果精確到個位．參考數據：≈1.4，≈1.7）

Answer 1

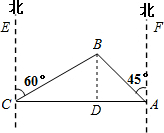解：過點B作BD⊥AC于D，
根據題意可得：EC⊥AC，FA⊥AC，∠ECB=60°，∠FAB=45°，
∴∠BCD=30°，∠BAD=45°，
在Rt△ABD中，AB=20（海里），
∴BD=AB•sin45°=20×=10（海里），
在Rt△BCD中，∠BCD=30°，
∴BC=2×10=20≈28（海里），
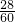∴護漁艦需小時可以到達該商船所在的位置C處，
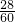∴×60=28（分鐘），
答：護漁艦約需28分鐘就可到達該漁船所在的位置C處．
分析：首先過點B作BD⊥AC于D，由題意可得：EC⊥AC，FA⊥AC，∠ECB=60°，∠FAB=45°，然后分別在Rt△ABD與Rt△BCD中，利用三角函數的性質，即可求得BC的長，繼而求得答案．
點評：此題考查了方向角問題．此題難度適中，解此題的關鍵是將方向角問題轉化為解直角三角形的知識，利用三角函數的知識求解．