
【題目】一次函數![]() 的圖像與x軸相交于點A,與y軸相交于點B,二次函數
的圖像與x軸相交于點A,與y軸相交于點B,二次函數![]() 圖像經過點A、B,與x軸相交于另一點C.
圖像經過點A、B,與x軸相交于另一點C.
(1)求a、b的值;
(2)在直角坐標系中畫出該二次函數的圖像;
(3)求∠ABC的度數.
【答案】(1)![]() ,b=6;(2)見解析;(3)∠ABC=45°
,b=6;(2)見解析;(3)∠ABC=45°
【解析】
(1)根據已知條件求得點A、點B的坐標,再代入二次函數的解析式,即可求得答案;
(2)根據列表、描點、依次連接即可畫出該二次函數的圖像;
(3)作AD⊥BC,利用兩點之間的距離公式求得![]() 的邊長,再運用面積法求高的方法求得AD,最后用特殊角的三角函數值求得答案.
的邊長,再運用面積法求高的方法求得AD,最后用特殊角的三角函數值求得答案.
(1)∵一次函數![]() 的圖像與x軸相交于點A,與y軸相交于點B,
的圖像與x軸相交于點A,與y軸相交于點B,
∴令![]() ,則
,則![]() ;令
;令![]() ,則
,則![]() ;
;
∴點A、點B的坐標分別為:![]() ,
,
∵二次函數![]() 圖像經過點A、B,
圖像經過點A、B,
∴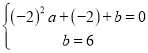 ,
,
解得:![]() ,
,
∴![]() ,b=6;
,b=6;
(2)由(1)知二次函數的解析式為:![]()
對稱軸為直線:![]() ,與x軸的交點為
,與x軸的交點為![]() .
.
x |
| -2 | -1 | 0 | 0.5 | 1 | 2 | 3 |
|
y |
| 0 | 4 | 6 | 0.25 | 6 | 4 | 0 |
|
二次函數的圖像如圖:
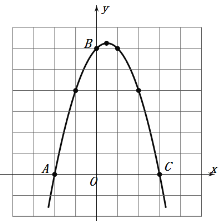
(3)如圖,過A作AD⊥BC于D,
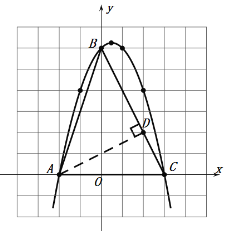
AB=![]() ,
,
CB=![]() ,
,
![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
解得:![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() .
.
故∠ABC=45°.


 培優三好生系列答案
培優三好生系列答案科目:初中數學 來源: 題型:
【題目】如圖為二次函數y=ax2+bx+c的圖象,在下列說法中①ac>0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3;③a+b+c<0;④當x>1時,y隨x的增大而增大,正確的是( )
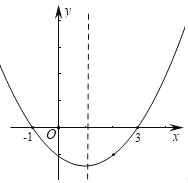
A. ①③B. ②④C. ①②④D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AC為圓O的直徑,弦AD的延長線與過點C的切線交于點B,E為BC中點,AC= ![]() ,BC=4.
,BC=4.
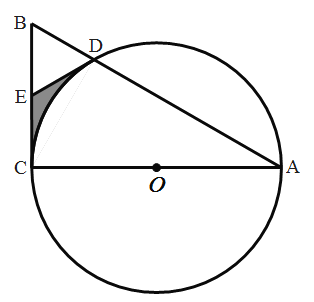
(1)求證:DE為圓O的切線;
(2)求陰影部分面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在平面直角坐標系中,拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() ,將直線
,將直線![]() 繞著點
繞著點![]() 順時針旋轉
順時針旋轉![]() 的度數后與該拋物線交于
的度數后與該拋物線交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),點
的左側),點![]() 是該拋物線上一點
是該拋物線上一點
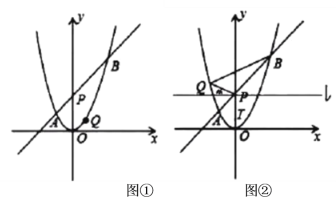
(1)若![]() ,求直線
,求直線![]() 的函數表達式
的函數表達式
(2)若點![]() 將線段分成
將線段分成![]() 的兩部分,求點
的兩部分,求點![]() 的坐標
的坐標
(3)如圖②,在(1)的條件下,若點![]() 在
在![]() 軸左側,過點
軸左側,過點![]() 作直線
作直線![]() 軸,點
軸,點![]() 是直線
是直線![]() 上一點,且位于
上一點,且位于![]() 軸左側,當以
軸左側,當以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似時,求
相似時,求![]() 的坐標
的坐標
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系![]() 中有點
中有點![]() 和某一函數圖象
和某一函數圖象![]() ,過點
,過點![]() 作
作![]() 軸的垂線,交圖象
軸的垂線,交圖象![]() 于點
于點![]() ,設點
,設點![]() ,
,![]() 的縱坐標分別為
的縱坐標分別為![]() ,
,![]() .如果
.如果![]() ,那么稱點
,那么稱點![]() 為圖象
為圖象![]() 的上位點;如果
的上位點;如果![]() ,那么稱點
,那么稱點![]() 為圖象
為圖象![]() 的圖上點;如果
的圖上點;如果![]() ,那么稱點
,那么稱點![]() 為圖象
為圖象![]() 的下位點.
的下位點.
(1)已知拋物線![]() .
.
① 在點A(-1,0),B(0,-2),C(2,3)中,是拋物線的上位點的是 ;
② 如果點![]() 是直線
是直線![]() 的圖上點,且為拋物線的上位點,求點
的圖上點,且為拋物線的上位點,求點![]() 的橫坐標
的橫坐標![]() 的取值范圍;
的取值范圍;
(2)將直線![]() 在直線
在直線![]() 下方的部分沿直線
下方的部分沿直線![]() 翻折,直線
翻折,直線![]() 的其余部分保持不變,得到一個新的圖象,記作圖象
的其余部分保持不變,得到一個新的圖象,記作圖象![]() .⊙
.⊙![]() 的圓心
的圓心![]() 在
在![]() 軸上,半徑為
軸上,半徑為![]() .如果在圖象
.如果在圖象![]() 和⊙
和⊙![]() 上分別存在點
上分別存在點![]() 和點F,使得線段EF上同時存在圖象
和點F,使得線段EF上同時存在圖象![]() 的上位點,圖上點和下位點,求圓心
的上位點,圖上點和下位點,求圓心![]() 的橫坐標
的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,PA、PB、CD是⊙O的切線,A、B、E是切點,CD分別交線段PA、PB于C、D兩點,若∠APB=40°,則∠COD的度數為( )
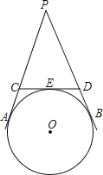
A.50°B.60°C.70°D.75°
查看答案和解析>>
科目:初中數學 來源: 題型:
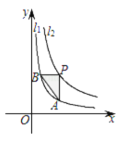
【題目】如圖,函數![]() (x>0)和
(x>0)和![]() (x>0)的圖象分別是
(x>0)的圖象分別是![]() 和
和![]() .設點P在
.設點P在![]() 上,PA∥y軸交
上,PA∥y軸交![]() 于點A,PB∥x軸,交
于點A,PB∥x軸,交![]() 于點B,△PAB的面積為( )
于點B,△PAB的面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知P為⊙O上一點,過點P作不過圓心的弦PQ,在劣弧PQ和優弧PQ上分別有點A、B(不與P、Q重合),連接AP、BP,若∠APQ=∠BPQ
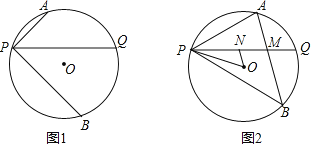
(1)如圖1,當∠APQ=45°,AP=1,BP=2![]() 時,求⊙O的半徑。
時,求⊙O的半徑。
(2)如圖2,連接AB,交PQ于點M,點N在線段PM上(不與P、M重合),連接ON、OP,設∠NOP=α,∠OPN=β,若AB平行于ON,探究α與β的數量關系。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1所示,![]() 六個小朋友圍成一圈(面向圈內)做傳球游戲,規定:球不得傳給自己,也不得傳給左手邊的人.若游戲中傳球和接球都沒有失誤.
六個小朋友圍成一圈(面向圈內)做傳球游戲,規定:球不得傳給自己,也不得傳給左手邊的人.若游戲中傳球和接球都沒有失誤.
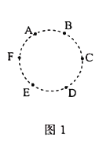
![]() 若由
若由![]() 開始一次傳球,則
開始一次傳球,則![]() 和
和![]() 接到球的概率分別是 、 ;
接到球的概率分別是 、 ;
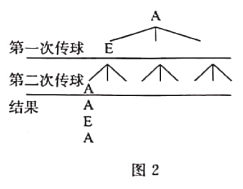
![]() 若增加限制條件:“也不得傳給右手邊的人”.現在球已傳到
若增加限制條件:“也不得傳給右手邊的人”.現在球已傳到![]() 手上,在下面的樹狀圖2中
手上,在下面的樹狀圖2中
畫出兩次傳球的全部可能情況,并求出球又傳到![]() 手上的概率.
手上的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com