
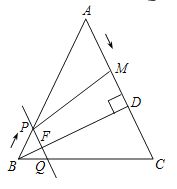
【題目】如圖,正方形![]() 和正方形
和正方形![]() 的頂點
的頂點![]() 在同一條直線上,頂點
在同一條直線上,頂點![]() 在同一條直線上.
在同一條直線上.![]() 是
是![]() 的中點,
的中點,![]() 的平分線
的平分線![]() 過點
過點![]() ,交
,交![]() 于點
于點![]() 連接
連接![]() 交
交![]() 于點
于點![]() 連接
連接![]() .以下四個結論:①
.以下四個結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
![]() ,其中正確的結論是____.
,其中正確的結論是____.
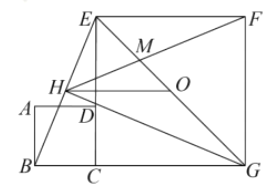
【答案】①②③
【解析】
①先利用正方形的性質證明![]() ,然后有
,然后有![]() ,通過等量代換可得
,通過等量代換可得![]() ,則
,則![]() ,即可判斷①的正誤;
,即可判斷①的正誤;
②通過直角三角形斜邊中線的性質得出點H在正方形CGFE的外接圓上,然后根據圓周角定理的推論得出![]() ,即可判斷②的正誤;
,即可判斷②的正誤;
③首先證明![]() ,則有
,則有![]() ,進而可得
,進而可得![]() ,由此可判斷③的正誤;
,由此可判斷③的正誤;
④先得出![]() 是
是![]() 的中位線,則
的中位線,則![]() ,然后根據平行線分線段成比例得出
,然后根據平行線分線段成比例得出 ![]() ,則有
,則有![]() ,進而可求出
,進而可求出![]() ,又因為
,又因為![]() ,則可判斷④的正誤.
,則可判斷④的正誤.
∵四邊形ABCD和四邊形CGFE是正方形,
∴![]() .
.
在![]() 和
和![]() 中,
中,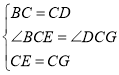
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,故①正確;
,故①正確;
![]() 是直角三角形,
是直角三角形,![]() 是
是![]() 的中點,
的中點,
![]() ,
,
![]() 點H在正方形CGFE的外接圓上.
點H在正方形CGFE的外接圓上.
![]() ,
,
![]() ,
,
![]() ,故②正確;
,故②正確;
∵GH平分![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,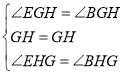
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,故③正確;
,故③正確;
∵四邊形CGFE是正方形,
∴![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() 是
是![]() 的中位線,
的中位線,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 與
與![]() 高相同,
高相同,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,故④錯誤.
,故④錯誤.
故答案為:①②③.


科目:初中數學 來源: 題型:
【題目】已知:如圖,在矩形ABCD中,點O在對角線BD上,以OD的長為半徑的⊙O與AD,BD分別交于點E、點F,且∠ABE=∠DBC.
(1)判斷直線BE與⊙O的位置關系,并證明你的結論;
(2)若sin∠ABE=![]() ,CD=2,求⊙O的半徑.
,CD=2,求⊙O的半徑.
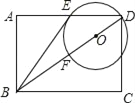
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小昕的口袋中有5把相似的鑰匙,其中2把鑰匙(記為A1,A2)能打開教室前門鎖,而剩余的3把鑰匙(記為B1,B2,B3)不能打開教室前門鎖.
(1)小昕從口袋中隨便摸出一把鑰匙就能打開教室前門鎖的概率是 ;
(2)請用樹狀圖或列表等方法,求出小昕從口袋中第一次隨機摸出的一把鑰匙不能打開教室前門鎖(摸出的鑰匙不再放回),而第二次隨機摸出的一把鑰匙正好能打開教室前門鎖的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】本學期,大興區開展了“恰同學少年,品詩詞美韻”中華傳統詩詞大賽活動![]() 小江統計了班級30名同學四月份的詩詞背誦數量,具體數據如表所示:
小江統計了班級30名同學四月份的詩詞背誦數量,具體數據如表所示:
詩詞數量 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人數 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
那么這30名同學四月份詩詞背誦數量的眾數和中位數分別是![]()
![]()
A. 11,7 B. 7,5 C. 8,8 D. 8,7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在Rt△ABC中,∠ACB=90°,點P以每秒1cm的速度從點A出發,沿折線AC-CB運動,到點B停止.過點P作PD⊥AB,垂足為D,PD的長y(cm)與點P的運動時間x(秒)的函數圖象如圖2所示.當點P運動5秒時,PD的長是( )
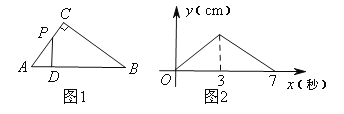
A.1.5cmB.1.2cmC.1.8cmD.2cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為2的等邊△ABC和邊長為1的等邊△A′B′C′,它們的邊B′C′,BC位于同一條直線l上,開始時,點C′與B重合,△ABC固定不動,然后把△A′B′C′自左向右沿直線l平移,移出△ABC外(點B′與C重合)停止,設△A′B′C′平移的距離為x,兩個三角形重合部分的面積為y,則y關于x的函數圖象是( )

A. 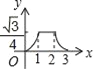 B.
B.  C.
C. 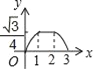 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形OABC的對角線OB,AC相交于點D,OA=3,OC=2,且BE∥AC,AE∥OB.
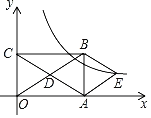
(1)求證:四邊形AEBD是菱形;
(2)求經過點E的雙曲線對應的函數解析式;
(3)設經過點E的雙曲線與直線BE的另一交點為F,過點F作x軸的平行線,交經過點B的雙曲線于點G,交y軸于點H,求△OFG的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A在∠MON的邊ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求證:四邊形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的長;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 于
于![]() ,且
,且![]() .點
.點![]() 從點
從點![]() 出發,沿
出發,沿![]() 方向勻速運動,速度為
方向勻速運動,速度為![]() ;同時直線
;同時直線![]() 由點
由點![]() 出發沿
出發沿![]() 方向勻速運動,速度為
方向勻速運動,速度為![]() ,運動過程中始終保持
,運動過程中始終保持![]() ,直線
,直線![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,連接
,連接![]() ,設運動時間為
,設運動時間為![]() .
.
(1)![]() ___________,
___________,![]() __________,
__________,![]() _____________;(用含
_____________;(用含![]() 的式子表示)
的式子表示)
(2)當四邊形![]() 是平行四邊形時,求
是平行四邊形時,求![]() 的值;
的值;
(3)當點![]() 在線段
在線段![]() 的垂直平分線上時,求
的垂直平分線上時,求![]() 的值;
的值;
(4)是否存在時刻![]() ,使以
,使以![]() 為直徑的圓與
為直徑的圓與![]() 的邊相切?若存在,直接寫出
的邊相切?若存在,直接寫出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com