
【題目】如圖,在等邊三角形ABC中,點E、D分別從A、C出發,沿AC,CB方向以相同的速度在線段AC,CB上運動,AD、BE相交于F點. 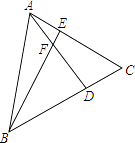
(1)求證:△ABE≌△CAD;
(2)當E、D運動時,∠BFD大小是否發生改變?若不變求其大小,若改變求其變化范圍.
【答案】
(1)解:∵△ABC是等邊三角形,
∴AC=AB,∠C=∠BAE=60°,
∵點E、D分別從A、C出發,沿AC,CB方向以相同的速度在線段AC,CB上運動,
∴BD=CE,
∴AE=CD,
在△ABE和△CAD中,
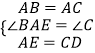 ,
,
∴△ABE≌△CAD
(2)解:當E、D運動時,∠BFD大小不發生改變,
∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∵∠AFE=∠ABE+∠BAF,
∴∠AFE=∠CAD+∠BAF=∠BAC=60°,
∵∠AFE=∠BFD(對頂角相等),
∴∠BFD=60°
【解析】(1)由等邊三角形ABC可得出的條件是:AB=AC,∠BAC=∠ACB=60°,可根據SAS證明△ABE≌△CAD;(2)E、D運動時,∠BFD大小不發生改變,根據△ABE≌△CAD,得到∠ABE=∠CAD,利用外角的性質得到∠AFE=∠ABE+∠BAF,再根據對頂角相等,即可解答.
【考點精析】根據題目的已知條件,利用等邊三角形的性質的相關知識可以得到問題的答案,需要掌握等邊三角形的三個角都相等并且每個角都是60°.


 華東師大版一課一練系列答案
華東師大版一課一練系列答案科目:初中數學 來源: 題型:
【題目】在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分線,垂足為D點,交AC于點E. 
(1)若∠ABE=38°,求∠EBC的度數;
(2)若△ABC的周長為36cm,一邊為13cm,求△BCE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中正確的是 ( )
A. 變量 x , y 滿足 x + 3y = 1 ,則 y 是 x 的函數
B. 變量 x , y 滿足![]() ,則 y 是 x 的函數
,則 y 是 x 的函數
C. 變量 x , y 滿足∣ y ∣= x ,則 y 是 x 的函數
D. 變量 x , y 滿足 y2 = x ,則 y 是 x 的函數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=mx與雙曲線y=![]() 相交于A、B兩點,A點的坐標為(1,2)
相交于A、B兩點,A點的坐標為(1,2)
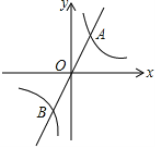
(1)求反比例函數的表達式;
(2)根據圖象直接寫出當mx>![]() 時,x的取值范圍;
時,x的取值范圍;
(3)計算線段AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校舉行全體學生“漢字聽寫”比賽,每位學生聽寫漢字![]() 個.隨機抽取了部分學生的聽寫結果,繪制成如下的圖表:
個.隨機抽取了部分學生的聽寫結果,繪制成如下的圖表:
組別 | 正確字數 | 人數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根據以上信息完成下列問題:
(![]() )統計表中的
)統計表中的![]() __________,
__________,![]() __________,并補全直方圖.
__________,并補全直方圖.
(![]() )扇形統計圖中“
)扇形統計圖中“![]() 組”所對應的圓心角的度數是__________.
組”所對應的圓心角的度數是__________.
(![]() )已知該校共有
)已知該校共有![]() 名學生,如果聽寫正確的字的個數少于
名學生,如果聽寫正確的字的個數少于![]() 個定為不合格,請你估計該校本次聽寫比賽不合格的學生人數.
個定為不合格,請你估計該校本次聽寫比賽不合格的學生人數.
各組別人數分布比例 | |
|
|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市南縣大力發展農村旅游事業,全力打造“洞庭之心濕地公園”,其中羅文村的“花海、涂鴉、美食”特色游享譽三湘,游人如織.去年村民羅南洲抓住機遇,返鄉創業,投入20萬元創辦農家樂(餐飲+住宿),一年時間就收回投資的80%,其中餐飲利潤是住宿利潤的2倍還多1萬元.
(1)求去年該農家樂餐飲和住宿的利潤各為多少萬元?
(2)今年羅南洲把去年的餐飲利潤全部用于繼續投資,增設了土特產的實體店銷售和網上銷售項目.他在接受記者采訪時說:“我預計今年餐飲和住宿的利潤比去年會有10%的增長,加上土特產銷售的利潤,到年底除收回所有投資外,還將獲得不少于10萬元的純利潤.”請問今年土特產銷售至少有多少萬元的利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料并填空:
在平面直角坐標系![]() 中,點
中,點![]() 經過變換
經過變換![]() 得到點
得到點![]() ,變換記作
,變換記作![]() ,其中
,其中![]() (
(![]() ,
, ![]() 為常數).例如,當
為常數).例如,當![]() ,且
,且![]() 時,
時, ![]() .
.
(![]() )當
)當![]() ,且
,且![]() 時,
時, ![]() __________.
__________.
(![]() )若
)若![]() ,則
,則![]() __________,
__________, ![]() __________.
__________.
(![]() )設點
)設點![]() 的坐標滿足
的坐標滿足![]() ,點
,點![]() 經過變換
經過變換![]() 得到點
得到點![]() ,若點
,若點![]() 到點
到點![]() 重合,求
重合,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com