
 交y軸于點A,交x軸正半軸于點B.
交y軸于點A,交x軸正半軸于點B.
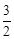 時, 則MN﹣PQ<0,即MN<PQ;
時, 則MN﹣PQ<0,即MN<PQ;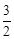 時, 則MN﹣PQ=0,即MN=PQ;
時, 則MN﹣PQ=0,即MN=PQ;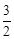 <m<3時,則MN﹣PQ>0,即MN>PQ。
<m<3時,則MN﹣PQ>0,即MN>PQ。 ,解得,
,解得,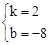 。
。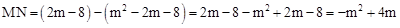 ;
;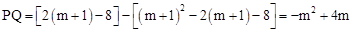 。
。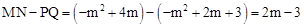 。
。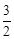 時, 則MN﹣PQ<0,即MN<PQ;
時, 則MN﹣PQ<0,即MN<PQ;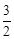 時, 則MN﹣PQ=0,即MN=PQ;
時, 則MN﹣PQ=0,即MN=PQ;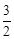 <m<3時,則MN﹣PQ>0,即MN>PQ。
<m<3時,則MN﹣PQ>0,即MN>PQ。

 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

 )
)查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 。
。 。
。查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
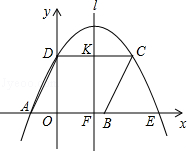
 與x軸相交于B(1,0)、C(4,0)兩點,與y軸的正半軸相交于A點,過A、B、C三點的⊙P與y軸相切于點A.M為y軸負半軸上的一個動點,直線MB交⊙P于點D,交拋物線于點N。
與x軸相交于B(1,0)、C(4,0)兩點,與y軸的正半軸相交于A點,過A、B、C三點的⊙P與y軸相切于點A.M為y軸負半軸上的一個動點,直線MB交⊙P于點D,交拋物線于點N。
 ,求N點坐標;
,求N點坐標;查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
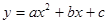 的圖象開口向上,圖象經過點(-1,2)和(1,0),且與
的圖象開口向上,圖象經過點(-1,2)和(1,0),且與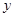 軸交于負半軸.給出四個結論:①abc<0;②2a+
軸交于負半軸.給出四個結論:①abc<0;②2a+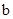 >0;③a+c=1; ④a>1.其中正確結論的序號是 (將你認為正確結論的序號都填上) .
>0;③a+c=1; ④a>1.其中正確結論的序號是 (將你認為正確結論的序號都填上) .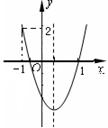
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
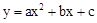 (a≠0)的圖象與x軸交于A、B兩點,與y軸交于C點,且對稱軸為x=1,點B坐標為(﹣1,0).則下面的四個結論:①2a+b=0;②4a-2b+c<0;③ac>0;④當y<0時,x<-1或x>2.其中正確的個數是
(a≠0)的圖象與x軸交于A、B兩點,與y軸交于C點,且對稱軸為x=1,點B坐標為(﹣1,0).則下面的四個結論:①2a+b=0;②4a-2b+c<0;③ac>0;④當y<0時,x<-1或x>2.其中正確的個數是
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com