Question

已知二次函數y=ax²+bx+c的圖象經過點A（3，0），B（2，-3），C（0，-3）。
（1）求此函數的解析式及圖象的對稱軸；
（2）點P從B點出發以每秒0.1個單位的速度沿線段BC向C點運動，點Q從O點出發以相同的速度沿線段OA向A點運動，其中一個動點到達端點時，另一個也隨之停止運動，設運動時間為t秒。
①當t為何值時，四邊形ABPQ為等腰梯形；
②設PQ與對稱軸的交點為M，過M點作x軸的平行線交AB于點N，設四邊形ANPQ的面積為S，求面積S關于時間t的函數解析式，并指出t的取值范圍；當t為何值時，S有最大值或最小值。

Answer 1

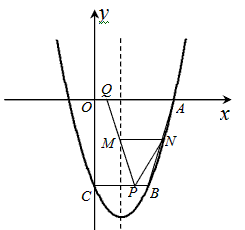
解：（1）∵二次函數的圖象經過點C（0，-3）， ∴c=-3， 將點A（3，0），B（2，-3）代入得， 解得：a=1，b=-2， ∴， 配方得：， 所以對稱軸為x=1；
（2）由題意可知：BP= OQ=0.1t， ∵點B，點C的縱坐標相等， ∴BC∥OA， 過點B，點P作BD⊥OA，PE⊥OA，垂足分別為D，E， 要使四邊形ABPQ為等腰梯形，只需PQ=AB，即QE=AD=1， 又QE=OE-OQ=（2-0.1t）-0.1t=2-0.2t， ∴2-0.2t=1， 解得t=5， 即t=5秒時，四邊形ABPQ為等腰梯形， ②設對稱軸與BC，x軸的交點分別為F，G， ∵對稱軸x=1是線段BC的垂直平分線， ∴BF=CF=OG=1， 又∵BP=OQ， ∴PF=QG， 又∵∠PMF=∠QMG， ∴△MFP≌△MGQ， ∴MF=MG， ∴點M為FG的中點， ∴S==， 由 ∴S= 又BC=2，OA=3， ∴點P運動到點C時停止運動，需要20秒， ∴0＜t≤20， ∴當t=20秒時，面積S有最小值3。