
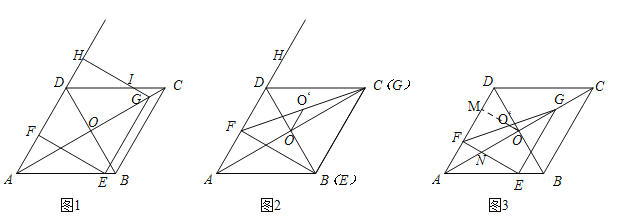
【題目】如圖,在菱形ABCD中,對角線AC與BD相交于點O,AB=8,∠BAD=60°,點E從點A出發,沿AB以每秒2個單位長度的速度向終點B運動,當點E不與點A重合時,過點E作EF⊥AD于點F,作EG∥AD交AC于點G,過點G作GH⊥AD交AD(或AD的延長線)于點H,得到矩形EFHG,設點E運動的時間為t秒
(1)求線段EF的長(用含t的代數式表示);
(2)求點H與點D重合時t的值;
(3)設矩形EFHG與菱形ABCD重疊部分圖形的面積與S平方單位,求S與t之間的函數關系式;
(4)矩形EFHG的對角線EH與FG相交于點O′,當OO′∥AD時,t的值為 ;當OO′⊥AD時,t的值為 .

【答案】(1)EF=![]() t;(2)t=
t;(2)t=![]() ;(3)
;(3)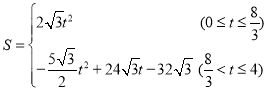 ;(4)t=4;t=3.
;(4)t=4;t=3.
【解析】
試題分析:(1)由題意知:AE=2t,由銳角三角函數即可得出EF=![]() t;
t;
(2)當H與D重合時,FH=GH=8﹣t,由菱形的性質和EG∥AD可知,AE=EG,解得t=![]() ;
;
(3)矩形EFHG與菱形ABCD重疊部分圖形需要分以下兩種情況討論:①當H在線段AD上,此時重合的部分為矩形EFHG;②當H在線段AD的延長線上時,重合的部分為五邊形;
(4)當OO′∥AD時,此時點E與B重合;當OO′⊥AD時,過點O作OM⊥AD于點M,EF與OA相交于點N,然后分別求出O′M、O′F、FM,利用勾股定理列出方程即可求得t的值.
試題解析:(1)由題意知:AE=2t,0≤t≤4,∵∠BAD=60°,∠AFE=90°,∴sin∠BAD=![]() ,∴EF=
,∴EF=![]() t;
t;
(2)∵AE=2t,∠AEF=30°,∴AF=t,當H與D重合時,此時FH=8﹣t,∴GE=8﹣t,∵EG∥AD,∴∠EGA=30°,∵四邊形ABCD是菱形,∴∠BAC=30°,∴∠BAC=∠EGA=30°,∴AE=EG,∴2t=8﹣t,∴t=![]() ;
;
(3)當0≤t≤![]() 時,此時矩形EFHG與菱形ABCD重疊部分圖形為矩形EFHG,∴由(2)可知:AE=EG=2t,∴S=EFEG=
時,此時矩形EFHG與菱形ABCD重疊部分圖形為矩形EFHG,∴由(2)可知:AE=EG=2t,∴S=EFEG=![]() t2t=
t2t=![]() ;
;
當![]() <t≤4時,如圖1,設CD與HG交于點I,此時矩形EFHG與菱形ABCD重疊部分圖形為五邊形FEGID,∵AE=2t,∴AF=t,EF=
<t≤4時,如圖1,設CD與HG交于點I,此時矩形EFHG與菱形ABCD重疊部分圖形為五邊形FEGID,∵AE=2t,∴AF=t,EF=![]() t,∴DF=8﹣t,∵AE=EG=FH=2t,∴DH=2t﹣(8﹣t)=3t﹣8,∵∠HDI=∠BAD=60°,∴tan∠HDI=
t,∴DF=8﹣t,∵AE=EG=FH=2t,∴DH=2t﹣(8﹣t)=3t﹣8,∵∠HDI=∠BAD=60°,∴tan∠HDI=![]() ,∴HI=
,∴HI=![]() DH,∴S=EFEG﹣
DH,∴S=EFEG﹣![]() DHHI=
DHHI=![]() =
=![]() ;
;
綜上所述: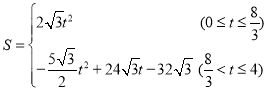 ;
;
(4)當OO′∥AD時,如圖2,此時點E與B重合,∴t=4;
當OO′⊥AD時,如圖3,過點O作OM⊥AD于點M,EF與OA相交于點N,由(2)可知:AF=t,AE=EG=2t,∴FN=![]() t,FM=t,∵O′O⊥AD,O′是FG的中點,∴O′O是△FNG的中位線,∴O′O=
t,FM=t,∵O′O⊥AD,O′是FG的中點,∴O′O是△FNG的中位線,∴O′O=![]() FN=
FN=![]() t,∵AB=8,∴由勾股定理可求得:OA=
t,∵AB=8,∴由勾股定理可求得:OA=![]() ,∴OM=
,∴OM=![]() ,∴O′M=
,∴O′M=![]() ,∵FE=
,∵FE=![]() t,EG=2t,∴由勾股定理可求得:
t,EG=2t,∴由勾股定理可求得:![]() ,∴由矩形的性質可知:
,∴由矩形的性質可知:![]() ,∵由勾股定理可知:
,∵由勾股定理可知:![]() ,∴
,∴![]() ,∴t=3或t=﹣6(舍去).
,∴t=3或t=﹣6(舍去).
故答案為:t=4;t=3.


 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:初中數學 來源: 題型:
【題目】有A、B、C、D四位員工做一項工作,每天必須是三位員工同時做,另一位員工休息,當完成這項工作時,D做了8天,比其他任何人都多,B做了5天,比其他任何人都少,那么A做了_____天.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列去括號錯誤的是
A. a-(b+c)=a-b-c B. a+(b-c)=a+b-c
C. 2(a-b)=2a-b D. -(a-2b)=-a+2b
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業車間有50名工人,某一天他們生產的機器零件個數統計如表:
零件個數(個) | 6 | 7 | 8 |
人數(人) | 15 | 22 | 10 |
表中表示零件個數的數據中,眾數、中位數分別是( )
A.7個、7個B.6個、7個C.5個、6個D.8個、6個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com