
【題目】已知:如圖,直線a∥b,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,且
上,且![]() ,
,![]() .點
.點![]() 、
、![]() 從
從![]() 點同時出發,分別以1個單位/秒,2個單位/秒的速度,在直線b上沿相反方向運動.設運動
點同時出發,分別以1個單位/秒,2個單位/秒的速度,在直線b上沿相反方向運動.設運動![]() 秒后,得到△ACD.(友情提醒:本題的結果可用根號表示)
秒后,得到△ACD.(友情提醒:本題的結果可用根號表示)
(1)當![]() 秒時,點
秒時,點![]() 到直線
到直線![]() 的距離為 ;
的距離為 ;
(2)若△ACD是直角三角形,t的值為 ;
(3)若△ACD是等腰三角形,求t的值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)當t=
;(3)當t=![]() s或
s或![]() s時,△ACD為等腰三角形.
s時,△ACD為等腰三角形.
【解析】
(1)根據點到直線的距離是垂線段的長,求解即可.
(2)因為AB⊥b,所以∠ACB,∠ADB不可能等于90°,則只有∠CAD=90°,利用勾股定理列方程求解即可.
(3)因為BC<BD,所以 AC<AD,∴ 若△ACD是等腰三角形,則AD=CD或AC=CD, 分情況列方程求解即可.
解:(1)由題意得,BD=2×6=12,AB=5,
∵ AB⊥b,
∴ 在Rt△ABD中,
![]() =
=![]() =13,
=13,
設B到直線AD的距離是h,
則![]() ,
,
∴h=![]() ;
;
(2)∵AB⊥b,
∴∠ACB,∠ADB不可能等于90°
若△ACD是直角三角形,
則∠CAD=90°,且BC=t,BD=2t,CD=BC+BD=3t,
![]() ,
,
![]() ,
,
∴ 在Rt△ACD中,
![]() ,
,
∴25+t2+25+4t2=9 t2,
∴ t=![]() .
.
(3)∵BC<BD,
∴ AC<AD,
∴ 若△ACD是等腰三角形,則AD=CD或AC=CD,
若AD=CD,
由題意得,BC=t,BD=2t, ∴AD=CD=3t
在Rt△ABD中,AB=5, 由勾股定理可得:
BD2+AB2=AD2,即(2t)2+52=(3t)2 ,
即t2=5,所以t=![]() ,
,
當AC=CD時,
同理,在Rt△ABC中,AB=5,由勾股定理可得:
BC2+AB2=AC2,t2+52=(3t)2 ,
即t2=![]() ,所以t=
,所以t=![]() ,
,
綜上所述,當t=![]() s或
s或![]() s時,△ACD為等腰三角形.
s時,△ACD為等腰三角形.


科目:初中數學 來源: 題型:
【題目】依法納稅是每個公民應盡的義務.新稅法規定:居民個人的綜合所得,以每一納稅月收入減去費用5000元以及專項扣除、專項附加扣除和依法確定的其它扣除后的余額,為個人應納稅所得額.已知李先生某月的個人應納稅所得額比張先生的多1500元,個人所得稅稅率相同情況下,李先生的個人所得稅稅額為76.5元,而張先生的個人所得稅稅額為31.5元.求李先生和張先生應納稅所得額分別為多少元?![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知實數a,b,c滿足a+b=ab=c,有下列結論:①若c≠0,則![]() ;②若a=3,則b+c=9;③若c≠0,則(1-a)(1-b)=
;②若a=3,則b+c=9;③若c≠0,則(1-a)(1-b)=![]() ;④若c=5,則a2+b2=15. 其中正確的是( )
;④若c=5,則a2+b2=15. 其中正確的是( )
A. ①③④ B. ①②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O是直線AB上一點,∠COD=90°,OE、OF分別是∠COB、∠AOD的平分線,且∠COB:∠AOD=4:9.
(1)寫出圖中∠BOD的余角和補角;
(2)求∠AOC的度數

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,矩形OABC的邊OA在x軸上,邊OC在y軸上,點B的坐標為(1,3),將矩形沿對角線AC翻折,B點落在D點的位置,且AD交y軸于點E,那么點D的坐標為() 
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(背景知識)
數軸是初中數學的一個重要工具,利用數軸可以將數與形完美結合.研究數軸我們發現有許多重要的規律:
例如,若數軸上![]() 點、
點、![]() 點表示的數分別為
點表示的數分別為![]() 、
、![]() ,則
,則![]() 、
、![]() 兩點之間的距離
兩點之間的距離![]() ,線段
,線段![]() 的中點
的中點![]() 表示的數為
表示的數為![]() .
.
(問題情境)
在數軸上,點![]() 表示的數為-20,點
表示的數為-20,點![]() 表示的數為10,動點
表示的數為10,動點![]() 從點
從點![]() 出發沿數軸正方向運動,同時,動點
出發沿數軸正方向運動,同時,動點![]() 也從點
也從點![]() 出發沿數軸負方向運動,已知運動到4秒鐘時,
出發沿數軸負方向運動,已知運動到4秒鐘時,![]() 、
、![]() 兩點相遇,且動點
兩點相遇,且動點![]() 、
、![]() 運動的速度之比是
運動的速度之比是![]() (速度單位:單位長度/秒).
(速度單位:單位長度/秒).
![]()
![]()
備用圖
(綜合運用)
(1)點![]() 的運動速度為______單位長度/秒,點
的運動速度為______單位長度/秒,點![]() 的運動速度為______單位長度/秒;
的運動速度為______單位長度/秒;
(2)當![]() 時,求運動時間;
時,求運動時間;
(3)若點![]() 、
、![]() 在相遇后繼續以原來的速度在數軸上運動,但運動的方向不限,我們發現:隨著動點
在相遇后繼續以原來的速度在數軸上運動,但運動的方向不限,我們發現:隨著動點![]() 、
、![]() 的運動,線段
的運動,線段![]() 的中點
的中點![]() 也隨著運動.問點
也隨著運動.問點![]() 能否與原點重合?若能,求出從
能否與原點重合?若能,求出從![]() 、
、![]() 相遇起經過的運動時間,并直接寫出點
相遇起經過的運動時間,并直接寫出點![]() 的運動方向和運動速度;若不能,請說明理由.
的運動方向和運動速度;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合題。
(1)如圖1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的長. 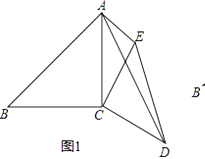
(2)如圖2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的長. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四張編號為A,B,C,D的卡片(除編號外,其余完全相同)的正面分別寫上如圖所示的正整數后,背面向上,洗勻放好. 
(1)我們知道,滿足a2+b2=c2的三個正整數a,b,c成為勾股數,嘉嘉從中隨機抽取一張,求抽到的卡片上的數是勾股數的概率P1;
(2)琪琪從中隨機抽取一張(不放回),再從剩下的卡片中隨機抽取一張(卡片用A,B,C,D表示).請用列表或畫樹形圖的方法求抽到的兩張卡片上的數都是勾股數的概率P2 , 并指出她與嘉嘉抽到勾股數的可能性一樣嗎?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com